
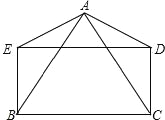
【题目】如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.求证:四边形BCDE是矩形.
【答案】证明见解析.
【解析】
试题分析:求出∠BAE=∠CAD,证△BAE≌△CAD,推出∠BEA=∠CDA,BE=CD,得出平行四边形BCDE,根据平行线性质得出∠BED+∠CDE=180°,求出∠BED,根据矩形的判定求出即可.
试题解析:∵∠BAD=∠CAE,
∴∠BAD-∠BAC=∠CAE-∠BAC,
∴∠BAE=∠CAD,
∵在△BAE和△CAD中

∴△BAE≌△CAD(SAS),
∴∠BEA=∠CDA,BE=CD,
∵DE=CB,
∴四边形BCDE是平行四边形,
∵AE=AD,
∴∠AED=∠ADE,
∵∠BEA=∠CDA,
∴∠BED=∠CDE,
∵四边形BCDE是平行四边形,
∴BE∥CD,
∴∠CDE+∠BED=180°,
∴∠BED=∠CDE=90°,
∴四边形BCDE是矩形.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米.
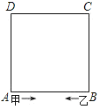
(1)出发后 分钟时,甲乙两人第一次在正方形的顶点处相遇;
(2)如果用记号(a,b)表示两人行了a分钟,并相遇过b次,那么当两人出发后第一次处在正方形的两个相对顶点位置时,对应的记号应是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法中正确的说法的个数是( )
①无理数就是开方开不尽的数;
②无理数是无限不循环小数;
③无理数包括正无理数,零,负无理数;
④无理数都可以用数轴上的点来表示.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中原命题和逆命题都正确的是( )
A. 对顶角相等 B. 两直线平行,同旁内角相等
C. 全等三角形的对应角相等 D. 全等三角形的对应边相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,与点(﹣5,8)关于y轴对称的点的坐标是( )
A. (5,﹣8) B. (﹣5,﹣8) C. (5,8) D. (8,﹣5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com