
【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点的坐标分别为A (0,2),B(﹣1,0),点C为线段AB的中点,现将线段BA绕点B按逆时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)、经过点D.
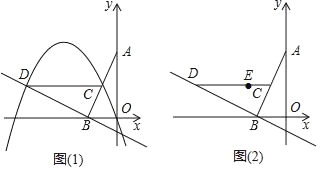
(1)如图1,若该抛物线经过原点O,且a=﹣1.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由.
(2)如图2,若该抛物线y=ax2+bx+c(a<0)经过点E(﹣1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余,若符合条件的Q点的个数是4个,请直接写出a的取值范围 .
【答案】(1)①D(﹣3,1),抛物线的表达式为:y=﹣x2﹣![]() x;②存在,点P的坐标为:P(﹣
x;②存在,点P的坐标为:P(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() );(2)a<﹣
);(2)a<﹣![]() 或a>1+
或a>1+![]() 或﹣
或﹣![]() <a<1-
<a<1-![]() .
.
【解析】
(1)①为A (0,2),B(-1,0),BA绕点B按逆时针方向旋转90°得到线段BD,把原点坐标、点D坐标、a=-1代入抛物线方程,即可求解;
②如下图所示,∠QOB与∠BCD互余,直线OP的方程为y=-![]() x,将直线方程与抛物线方程联立即可求解,当P在x轴上方时,用同样的方法可以求解;
x,将直线方程与抛物线方程联立即可求解,当P在x轴上方时,用同样的方法可以求解;
(2)把D、E坐标代入抛物线方程,解得:y=ax2+4ax+(3a+1),①当a<0时,若符合条件的Q点的个数是4个,则Q点在x轴上下各2个,则3a+1<0,然后分Q在x轴上方和x轴下方时两种情况即可求解,同样可以求出a>0的情况.
(1)为A (0,2),B(﹣1,0),
①点C为线段AB的中点,则C(-![]() ,1),
,1),
BA绕点B按逆时针方向旋转90°得到线段BD,
则D(﹣3,1),∴DC∥x轴,
把原点坐标、点D坐标、a=﹣1代入抛物线方程,
解得:抛物线的表达式为:y=﹣x2﹣![]() x…①;
x…①;
②如下图所示,∠QOB与∠BCD互余,
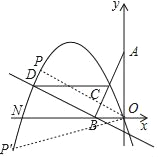
当P在x轴上方时,OP⊥AB,
直线AB的k值为2,则直线OP的k值为﹣![]() ,
,
直线OP的方程为y=﹣![]() x…②,
x…②,
①、②联立并整理得:x=0(舍去),x=﹣![]() ,
,
则点P(﹣![]() ,
,![]() );
);
当P在x轴上方时,
直线OP的方程为y=![]() x…③,
x…③,
①、③联立并整理得:x=0(舍去),x=﹣![]() ,
,
则P′(﹣![]() ,﹣
,﹣![]() );
);
故:存在,点P的坐标为:P(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() );
);
(2)把D、E坐标代入抛物线方程,
解得:y=ax2+4ax+(3a+1)…④,
函数与y轴交点的纵坐标为:3a+1
有(2)知:当Q在x轴上方时,OQ的方程为:y=﹣![]() x…⑤,
x…⑤,
当Q在x轴下方时,OQ的方程为:y=![]() x…⑥,
x…⑥,
①当a<0时,若符合条件的Q点的个数是4个,则Q点在x轴上下各2个,则3a+1<0,即:![]() ,
,
Q在x轴上方时,联立④、⑤得:-![]() x=ax2+4ax+(3a+1),△=4a2+
x=ax2+4ax+(3a+1),△=4a2+![]() >0,即:必定有2个Q点,
>0,即:必定有2个Q点,
Q在x轴下方时,联立④、⑥得:x=ax2+4ax+(3a+1),△=4a2﹣8a+![]() >0,a>1+
>0,a>1+![]() 或a<1﹣
或a<1﹣![]() ,
,
故:a<﹣![]() ;
;
②当a<0时,若符合条件的Q点的个数是4个,则Q点在x轴上下各2个,则3a+1>0,即:a>﹣![]() ,
,
Q在x轴上方时,联立④、⑤得:-![]() x=ax2+4ax+(3a+1),△=4a2+
x=ax2+4ax+(3a+1),△=4a2+![]() >0,即:必定有2个Q点,
>0,即:必定有2个Q点,
Q在x轴下方时,联立④、⑥得:x=ax2+4ax+(3a+1),△=4a2﹣8a+![]() >0,a>1+
>0,a>1+![]() 或a<1﹣
或a<1﹣![]() ,
,
故:a>1+![]() 或﹣
或﹣![]() <a<1-
<a<1-![]() .
.
综上所述:a<﹣![]() 或a>1
或a>1![]() 或﹣
或﹣![]() <a<1-
<a<1-![]() .
.


科目:初中数学 来源: 题型:
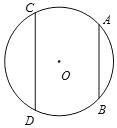
【题目】如图,直径为 10cm 的⊙O 中,两条弦 AB,CD 分别位于圆心的异侧,AB∥CD,且![]() ,若 AB=8cm,则 CD 的长为_____cm.
,若 AB=8cm,则 CD 的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
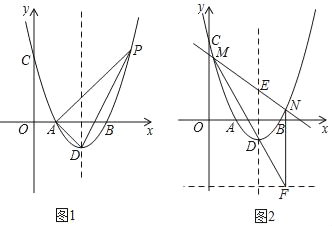
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,3),抛物线顶点为D点.
(1)求此抛物线解析式;
(2)如图1,点P为抛物线上的一个动点,且在对称轴右侧,若△ADP面积为3,求点P的坐标;
(3)在(2)的条件下,PA交对称轴于点E,如图2,过E点的任一条直线与抛物线交于M,N两点,直线MD交直线y=﹣3于点F,连结NF,求证:NF∥y轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
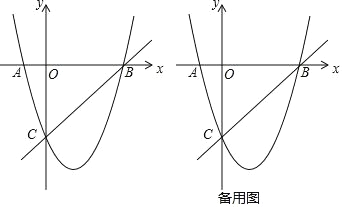
【题目】在平面直角坐标系中,二次函数的图象交坐标轴于 A(﹣1,0),B(4,0),C
(0,﹣4)三点,点 P 是直线 BC 下方抛物线上一动点.
(1) 求这个二次函数的解析式;
(2) 是否存在点 P,使△POC 是以 OC 为底边的等腰三角形?若存在,求出 P 点坐标;若不存在,请说明理由;
(3) 在抛物线上是否存在点 D(与点 A 不重合)使得 S△DBC=S△ABC,若存在,求出点 D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们约定:对角线互相垂直的凸四边形叫做“正垂形”.
(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“正垂形”的有 ;
②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形 “正垂形”.(填“是”或“不是”)
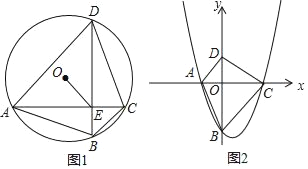
(2)如图1,A,B,C,D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,∠ACB﹣∠CDB=∠ACD﹣∠CBD,当![]() ≤OE≤
≤OE≤![]() 时,求AC2+BD2的取值范围;
时,求AC2+BD2的取值范围;
(3)如图2,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a,b,c为常数,a>0,c<0)与x轴交于A,C两点(点A在点C的左侧),B是抛物线与y轴的交点,点D的坐标为(0,﹣ac),记“正垂形”ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为S1,S2,S3,S4.试直接写出满足下列三个条件的抛物线的解析式;
①![]() ; ②
; ②![]() ; ③“正垂形”ABCD的周长为12
; ③“正垂形”ABCD的周长为12![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长都是![]() 的正方形网格中,
的正方形网格中,![]() 的三个顶点都在小正方形的格点上.将
的三个顶点都在小正方形的格点上.将![]() 绕点
绕点![]() 旋转
旋转![]() 得到
得到![]() (点
(点![]() 、
、![]() 分别与点
分别与点![]() 、
、![]() 对应),连接
对应),连接![]() ,
,![]() .
.
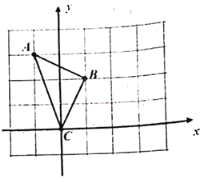
(1)请直接在网格中补全图形;
(2)四边形![]() 的周长是________________(长度单位)
的周长是________________(长度单位)
(3)直接写出四边形![]() 是何种特殊的四边形.
是何种特殊的四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与徒步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.
(1)求图中的a值.
(2)若在距离起点5千米处有一个地点C,此人从第一次经过点C到第二次经过点C,所用时间为1.75小时.
①求AB所在直线的函数解析式;
②请你直接回答,此人走完全程所用的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆假期期间,某单位8名领导和320名员工集体外出进行素质拓展活动,准备租用45座大车或30座小车.若租用2辆大车3辆小车共需租车费1700元;若租用3辆大车2辆小车共需租车费1800元
(1)求大、小车每辆的租车费各是多少元?
(2)若每辆车上至少要有一名领导,每个人均有座位,且总租车费用不超过3100元,求最省钱的租车方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com