
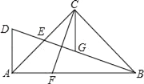
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上﹣点,连接CF,且∠ACF=∠CBG.
(1)求证:AF=CG;
(2)写出图中长度等于2DE的所有线段.
【答案】(1)详见解析;(2)长度等于2DE的线段有CF、BG、DG.
【解析】
(1)要证AF=CG,只需证明△AFC≌△CBG即可.
(2)延长CG交AB于H,则CH⊥AB,H平分AB,继而证得CH∥AD,得出DG=BG和△ADE与△CGE全等,从而证得CF=2DE.
证明:(1)∵∠ACB=90°,CG平分∠ACB,
∴∠ACG=∠BCG=45°,
又∵∠ACB=90°,AC=BC,
∴∠CAF=∠CBF=45°,
∴∠CAF=∠BCG,
在△AFC与△CGB中,
![]() ,
,
∴△AFC≌△CBG(ASA),
∴AF=CG;
(2)延长CG交AB于H,
∵CG平分∠ACB,AC=BC,
∴CH⊥AB,CH平分AB,
∵AD⊥AB,
∴AD∥CG,
∴∠D=∠EGC,
在△ADE与△CGE中,
![]() ,
,
∴△ADE≌△CGE(AAS),
∴DE=GE,
即DG=2DE,
∵AD∥CG,CH平分AB,
∴DG=BG,
∵△AFC≌△CBG,
∴CF=BG,
∴CF=2DE.
∵BG=CF,
∴BG=2DE,
∴DG=2DE,
故长度等于2DE的线段有CF、BG、DG.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】某物体从P点运动到Q点所用时间为7秒,其运动速度v(米每秒)关于时间t(秒)的函数关系如图所示.某学习小组经过探究发现:该物体前进3秒运动的路程在数值上等于矩形AODB的面积.由物理学知识还可知:该物体前t(3<t≤7)秒运动的路程在数值上等于矩形AODB的面积与梯形BDNM的面积之和. 根据以上信息,完成下列问题: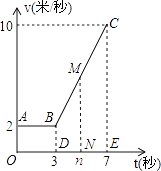
(1)当3<t≤7时,用含t的式子表示v;
(2)分别求该物体在0≤t≤3和3<t≤7时,运动的路程s(米)关于时间t(秒)的函数关系式;并求该物体从P点运动到Q总路程的 ![]() 时所用的时间.
时所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3.
<3.
∴![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ﹣2,
﹣2,
∴1<![]() ﹣1<2
﹣1<2
∴![]() ﹣1的整数部分为1.
﹣1的整数部分为1.
∴![]() ﹣1的小数部分为
﹣1的小数部分为![]() ﹣2
﹣2
解决问题:已知:a是![]() ﹣3的整数部分,b是
﹣3的整数部分,b是![]() ﹣3的小数部分,
﹣3的小数部分,
求:(1)a,b的值;
(2)(﹣a)3+(b+4)2的平方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则;等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.任何一个假分式都可以化成整式与真分式的和的形式,如: ![]() ;
; ![]()
(1)下列分式中,属于真分式的是:________(填序号);
①![]() ②
②![]() ③
③![]() ④
④![]()
(2)将假分式![]() 化成整式与真分式的和的形式:
化成整式与真分式的和的形式: ![]() =________+________;
=________+________;
(3)将假分式![]() 化成整式与真分式的和的形式:
化成整式与真分式的和的形式: ![]() =__________________.
=__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O,根据下列条件,求出∠BOC的度数.
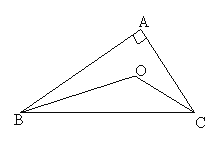
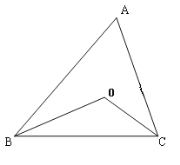
(1)已知∠ABC+∠ACB=100°,则∠BOC= .
(2)已知∠A=90°,求∠BOC的度数.
(3)从上述计算中,你能发现∠BOC与∠A的关系吗?请直接写出∠B0C与∠A的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC. 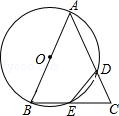
(1)求证:AB=AC;
(2)若AB=4,BC=2 ![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5).
(1)求三角形ABC的面积;
(2)如果三角形ABC的三个顶点的纵坐标不变,横坐标增加3个单位长度,得到三角形A1B1C1,试在图中画出三角形A1B1C1,并写出点A1,B1,C1的坐标;
(3)(2)中三角形A1B1C1与三角形ABC的大小、形状有什么关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
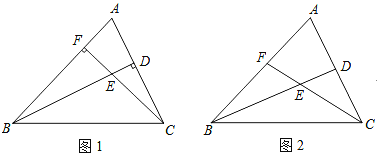
(1)若BD⊥AC,CF⊥AB,若BE=4,CE=2,求CD:BF;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,猜想∠BEC与∠A的数量关系;并说明理由.
(3)在(2)的条件下,若∠A=60°,试说明:BC=BF+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
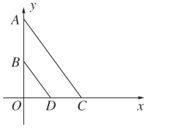
【题目】如图8,在平面直角坐标系xOy中,A(0,8),B(0,4),点C在x轴的正半轴上,点D为OC的中点.
(1)当BD与AC的距离等于2时,求线段OC的长;
(2)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线BD的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com