【题目】下列说法：①如果两个三角形全等，那么这两个三角形一定成轴对称；②数轴上的点和实数一一对应；③若
，则
；④两个无理数的和一定为无理数；⑤
精确到十分位；⑥如果一个数的算术平方根等于它本身，那么这个数是0.其中正确的说法有______.（填序号）
名校练考卷期末冲刺卷系列答案科目：初中数学 来源： 题型：
【题目】在小明、小红两名同学中选拔一人参加2018年张家界市“经典诗词朗诵”大赛，在相同的测试条件下，两人5次测试成绩（单位：分）如下：
小明：80，85，82，85，83 小红：88，79，90，81，72．
回答下列问题：
（1）求小明和小红测试的平均成绩；
（2）求小明和小红五次测试成绩的方差．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】"引葭赴岸“是《九章算木》中的- -道題:”今有池一丈 ,葭生其中央,出水一尺，引葭赴岸,迺与岸芥.伺水深,葭氏各几何?"題意是:有一个边长为10尺的正方形池塘，一棵芦苇AB生长在它的中央,高出水面BC为1尺.如果把该芦苓沿与水池边垂直的方向拉向岸辺,那么芦革的顶部B恰好碰到岸边的B'. 向芦苇长多少? (画出几何图形并解答)
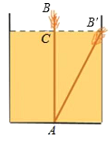
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将ABCD的AD边延长至点E，使DE＝
AD，连接CE，F是BC边的中点，连接FD．
(1)求证：四边形CEDF是平行四边形；
(2)若AB＝3，AD＝4，∠A＝60°，求CE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】函数
、
、
都是常数，且
叫做“奇特函数”，当
时，奇特函数
就成为反比例函数
是常数，且
．
若矩形的两边长分别是
、
，当两边长分别增加
、
后得到的新矩形的面积是
，求
与
的函数关系式，并判断这个函数是否“奇特函数”；
如图在直角坐标系中，点
为原点矩形
的顶点，
、
坐标分别为
、
，点
是
中点，连接
、
交于
，“奇特函数”
的图象经过点
、，求这个函数的解析式，并判断、、三点是否在这个函数图象上；
对于中的“奇特函数”的图象，能否经过适当的变换后与一个反比例函数图象重合，若能，请直接写出具体的变换过程和这个反比例函数解析式；若不能，请简述理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解题
（1）阅读理解：如图①，等边
内有一点
，若点到顶点
，
，
的距离分别为3，4，5，求
的大小.
思路点拨：考虑到
，
，
不在一个三角形中，采用转化与化归的数学思想，可以将
绕顶点逆时针旋转
到
处，此时
，这样，就可以利用全等三角形知识，结合已知条件，将三条线段的长度转化到一个三角形中，从而求出的度数.请你写出完整的解题过程.
（2）变式拓展：请你利用第（1）题的解答思想方法，解答下面问题：
已知如图②，中，
，
，
、
为
上的点且
，
，
，求
的大小.
（3）能力提升：如图③，在
中，
，
，
，点
为内一点，连接
，
，
，且
，请直接写出
的值，即
______.
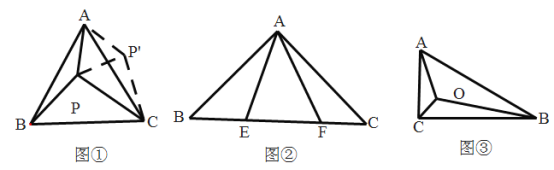
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有一个长为24米的篱笆，一面利用墙（墙的最大长度a为15米）围成的中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S平方米．
（1）求S与x的函数关系式；
（2）如果要使围成花圃面积最大，求AB的长为多少米？
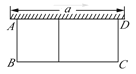
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
中，
厘米，
厘米，点
为
的中点．
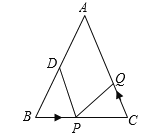
（1）如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1秒后，
与
是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等， 与是否可能全等？若能，求出全等时点Q的运动速度和时间；若不能，请说明理由．
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿三边运动，求经过多长时间点P与点Q第一次在的哪条边上相遇？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
