
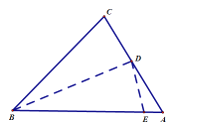
【题目】如图所示,在锐角三角形ABC中,AB=8,AC=5,BC=6,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,下列结论:①∠CBD=∠EBD,②DE⊥AB,③三角形ADE的周长是7,④![]() ,⑤
,⑤![]() .其中正确的个数有( )
.其中正确的个数有( )
A.2B.3C.4D.5
【答案】C
【解析】
根据翻折变换的性质得到DC=DE,BE=BC,![]() ,根据已知求出AE的长,根据三角形周长公式计算即可,根据高相等判断
,根据已知求出AE的长,根据三角形周长公式计算即可,根据高相等判断![]() ,根据△BCD△BDE判断①的对错,根据等高,则面积的比等于底边的比判断⑤.
,根据△BCD△BDE判断①的对错,根据等高,则面积的比等于底边的比判断⑤.
根据翻折变换的性质得到DC=DE,BE=BC=6,![]() ,
,
故DE⊥AB错误,即②错误
∴△BCD△BDE,
∴∠CBD=∠EBD,故①正确;
∵AB=8,∴AE=AB-BE=2,
△AED的周长为:AD+AE+DE=AC+AE=7,故③正确;
设三角形BCD的高为h,则三角形BAD的高也为h
∴ ,故④正确;
,故④正确;
当三角形BCD的高为H,底边为CD,则三角形BAD的高也为H,底边为AD
∴![]() ,故⑤正确.
,故⑤正确.
故选C.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
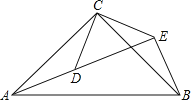
【题目】如图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=24,DE=17.
(1)求证:△CAD≌△CBE;
(2)求线段AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
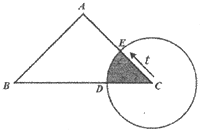
【题目】如图.在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,以每秒1单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,最符合扇形面积S关于运动时间t的变化趋势的是( )
A. 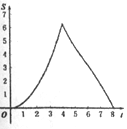 B.
B. 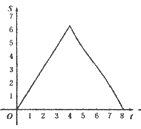
C. 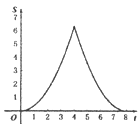 D.
D. 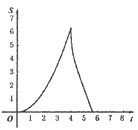
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 从
从![]() 点出发沿射线
点出发沿射线![]() 方向以每秒
方向以每秒![]() 个单位的速度向右运动.设点
个单位的速度向右运动.设点![]() 的运动时间为
的运动时间为![]() .连结
.连结![]() .
.
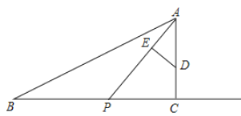
(1)当![]() 秒时,求
秒时,求![]() 的长度(结果保留根号);
的长度(结果保留根号);
(2)当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的值;
的值;
(3)过点![]() 做
做![]() 于点
于点![]() .在点
.在点![]() 的运动过程中,当
的运动过程中,当![]() 为何值时,能使
为何值时,能使![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
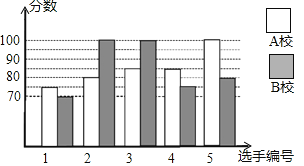
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
![]() 根据图示填写下表:
根据图示填写下表:
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
![]() 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
![]() 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
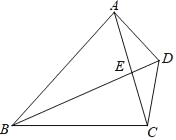
【题目】已知:如图,四边形ABCD的对角线AC和BD相交于点E,AD=DC,DC2=DEDB,求证:
(1)△BCE∽△ADE;
(2)ABBC=BDBE.
查看答案和解析>>
科目:初中数学 来源: 题型:
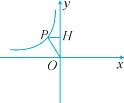
【题目】如图是反比例函数y=![]() 的图象的一支.
的图象的一支.
(1)求m的取值范围,并在图中画出另一支的图象;
(2)若m=-1,P(a,3)是双曲线上的一点,PH⊥y轴于H,将线段OP向右平移3PH的长度至O′P′,此时P的对应点P′恰好在另一条双曲线y=![]() 的图象上,则平移中线段OP扫过的面积为 ,k= .
的图象上,则平移中线段OP扫过的面积为 ,k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CG=EG
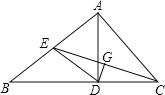
(1)求证:CD=AE;
(2)若AD=BD,CD=2,则求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x(度) | 0<x≤140 |
(2)小明家某月用电120度,需交电费 元
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com