
| A. | -2 | B. | -1 | C. | -$\frac{1}{2}$ | D. | 1 |
分析 由于AB长为定值,四边形ABCD周长最短其实就是AD+DC+BC最小不妨作出B点关于x轴的对称点B'(4,1),A点关于直线y=x的对称点A'(-2,-1)再连接A'B',该直线A'B'交x轴于C,交直线y=x于D,求出A′B′的解析式,把C、D点的坐标代入直线方程,求出m、n的值即可.
解答 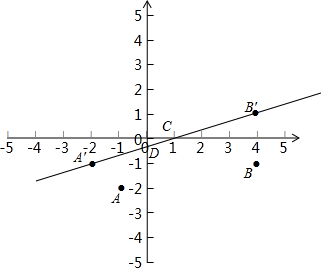 解:如图所示,作B点关于x轴的对称点B'(4,1),A点关于直线y=x的对称点A'(-2,-1)再连接A'B',该直线A'B'交x轴于C,交直线y=x于D,
解:如图所示,作B点关于x轴的对称点B'(4,1),A点关于直线y=x的对称点A'(-2,-1)再连接A'B',该直线A'B'交x轴于C,交直线y=x于D,
设直线A′B′的解析式为y=kx+b(k≠0),把点A'(-2,-1)、B'(4,1)代入得,
$\left\{\begin{array}{l}{-1=-2k+b}\\{1=4k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=-\frac{1}{3}}\end{array}\right.$,
故此函数的解析式为:y=$\frac{1}{3}$x-$\frac{1}{3}$,
分别把C(m,0),D(n,n)代入得,0=$\frac{1}{3}$m-$\frac{1}{3}$,n=$\frac{1}{3}$n-$\frac{1}{3}$,
即m=1,n=-$\frac{1}{2}$,
∴$\frac{m}{n}$=-2.
故选A.
点评 本题考查的是最短路线问题及用待定系数法求一次函数的解析式,利用轴对称的性质分别求出A′、B′两点的坐标是解答此题的关键.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
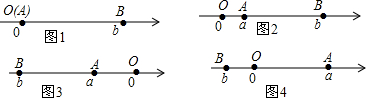
 某城区规划局为了方便居民的生活,计划在三个住宅小区A,B,C(如图所示) 之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场距离相等?
某城区规划局为了方便居民的生活,计划在三个住宅小区A,B,C(如图所示) 之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场距离相等?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
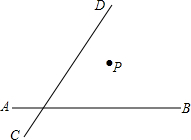 如图所示,P为马厩,AB为草地边缘(下方为草地),CD为一河流,牧人欲从马厩牵马先去草地吃草,然后到河边饮水,最后回到马厩,请帮他确定一条最佳行走路线.
如图所示,P为马厩,AB为草地边缘(下方为草地),CD为一河流,牧人欲从马厩牵马先去草地吃草,然后到河边饮水,最后回到马厩,请帮他确定一条最佳行走路线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com