
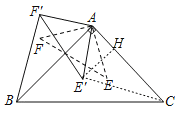
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃЌDЮЊБпABЩЯвЛЕуЃЌСЌНгCDЃЌдкЯпЖЮCDЩЯШЁвЛЕуEЃЌвдAEЮЊжБНЧБпзїЕШбќжБНЧЁїAEFЃЌЪЙЁЯEAFЃН90ЁуЃЌСЌНгBFНЛCDЕФбгГЄЯпгкЕуPЃЎ

ЃЈ1ЃЉЬНЫїЃКCEгыBFгаКЮЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃПВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєABЃН2ЃЌAEЃН1ЃЌАбЁїAEFШЦЕуAЫГЪБеыа§зЊжСЁїAE'FЁфЃЌЕБЁЯEЁфACЃН60ЁуЪБЃЌЧѓBFЁфЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉCEЃНBFЃЌCEЁЭBFЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЁАSASЁБПЩжЄЁїAECЁеЁїAFBЃЌПЩЕУCEЃНBFЃЌЁЯABFЃНЁЯACEЃЌНјЖјПЩЕУCEЁЭBFЃЛ
ЃЈ2ЃЉЙ§ЕуE'зїE'HЁЭACЃЌСЌНгE'CЃЌгЩжБНЧШ§НЧаЮЕФаджЪКЭЙДЙЩЖЈРэПЩЧѓE'CЕФГЄЃЌгЩЁАSASЁБПЩжЄЁїF'ABЁеЁїE'ACЃЌПЩЕУBF'ЃНCE'ЃН![]() ЃЎ
ЃЎ
ЃЈ1ЃЉCEЃНBFЃЌCEЁЭBFЃЌРэгЩШчЯТЃК
ЁпЁЯBACЃНЁЯEAFЃН90ЁуЃЌ
ЁрЁЯEACЃНЁЯFABЃЌ
гжЁпAEЃНAFЃЌABЃНACЃЌ
ЁрЁїAECЁеЁїAFBЃЈSASЃЉ
ЁрCEЃНBFЃЌЁЯABFЃНЁЯACEЃЌ
ЁпЁЯADCЃНЁЯBDPЃЌ
ЁрЁЯBPDЃНЁЯCADЃН90ЁуЃЌ
ЁрCEЁЭBFЃЛ
ЃЈ2ЃЉЙ§ЕуE'зїE'HЁЭACЃЌСЌНгE'CЃЌ
ЁпАбЁїAEFШЦЕуAЫГЪБеыа§зЊжСЁїAE'FЁфЃЌ
ЁрAFЃНAEЃНAE'ЃНAF'ЃН1ЃЌЁЯBAF'ЃНЁЯE'ACЃН60ЁуЃЌ
ЁпЁЯE'ACЃН60ЁуЃЌЁЯAHE'ЃН90ЁуЃЌ
ЁрЁЯAE'HЃН30ЁуЃЌ
ЁрAHЃН![]() AE'ЃН
AE'ЃН![]() ЃЌE'HЃН
ЃЌE'HЃН![]() AHЃН
AHЃН![]() ЃЌ
ЃЌ
ЁрHCЃНACЉAHЃН![]() ЃЌ
ЃЌ
ЁрE'CЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпAF'ЃНAE'ЃЌЁЯF'ABЃНЁЯE'ACЃН60ЁуЃЌABЃНACЃЌ
ЁрЁїF'ABЁеЁїE'ACЃЈSASЃЉ
ЁрBF'ЃНCE'ЃН![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§RtЁїBOCаББпЩЯЕФжаЕуAЃЌгыБпBCНЛгкЕуDЃЌСЌНгADЃЌдђЁїADBЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§RtЁїBOCаББпЩЯЕФжаЕуAЃЌгыБпBCНЛгкЕуDЃЌСЌНгADЃЌдђЁїADBЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
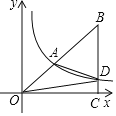
A.12B.16C.20D.24
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКдкЦНУцжБНЧзјБъЯЕжаЃЌЖдгкШЮвтСНЕу![]() ЃЌ
ЃЌ![]() ЃЌШєЕу
ЃЌШєЕу![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ![]() ЃЌФЧУДГЦЕу
ЃЌФЧУДГЦЕу![]() ЪЧЕу
ЪЧЕу![]() ЃЌ
ЃЌ![]() ЕФШкКЯЕу.
ЕФШкКЯЕу.
Р§ШчЃК![]() ЃЌ
ЃЌ![]() ЃЌЕБЕу
ЃЌЕБЕу![]() ТњЪЧ
ТњЪЧ![]() ЃЌ
ЃЌ![]() ЪБЃЌдђЕу
ЪБЃЌдђЕу![]() ЪЧЕу
ЪЧЕу![]() ЃЌ
ЃЌ![]() ЕФШкКЯЕуЃЌ
ЕФШкКЯЕуЃЌ

ЃЈ1ЃЉвбжЊЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧыЫЕУїЦфжавЛИіЕуЪЧСэЭтСНИіЕуЕФШкКЯЕу.
ЃЌЧыЫЕУїЦфжавЛИіЕуЪЧСэЭтСНИіЕуЕФШкКЯЕу.
ЃЈ2ЃЉШчЭМЃЌЕу![]() ЃЌЕу
ЃЌЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯШЮвтвЛЕуЃЌЕу
ЩЯШЮвтвЛЕуЃЌЕу![]() ЪЧЕу
ЪЧЕу![]() ЃЌ
ЃЌ![]() ЕФШкКЯЕу.
ЕФШкКЯЕу.
ЂйЪдШЗЖЈ![]() гы
гы![]() ЕФЙиЯЕЪН.
ЕФЙиЯЕЪН.
ЂкШєжБЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЕБ
ЃЌЕБ![]() ЮЊжБНЧШ§НЧаЮЪБЃЌЧѓЕу
ЮЊжБНЧШ§НЧаЮЪБЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
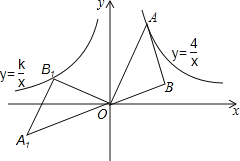
ЁОЬтФПЁПШчЭМЃЌAЪЧЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЭМЯѓЩЯвЛЕуЃЌвдOAЮЊаББпзїЕШбќжБНЧЁїABOЃЌНЋЁїABOШЦЕуOвдФцЪБеыа§зЊ135ЁуЃЌЕУЕНЁїA1B1OЃЌШєЗДБШР§КЏЪ§yЃН
ЃЈxЃО0ЃЉЭМЯѓЩЯвЛЕуЃЌвдOAЮЊаББпзїЕШбќжБНЧЁїABOЃЌНЋЁїABOШЦЕуOвдФцЪБеыа§зЊ135ЁуЃЌЕУЕНЁїA1B1OЃЌШєЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓОЙ§ЕуB1ЃЌдђkЕФжЕЪЧ_____ЃЎ
ЕФЭМЯѓОЙ§ЕуB1ЃЌдђkЕФжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЃЈaЁй0ЃЉНЛxжсгкAЁЂBСНЕуЃЌAЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ4ЃЉЃЌвдOCЁЂOAЮЊБпзїОиаЮOADCНЛХзЮяЯпгкЕуGЃЎ
ЃЈaЁй0ЃЉНЛxжсгкAЁЂBСНЕуЃЌAЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ4ЃЉЃЌвдOCЁЂOAЮЊБпзїОиаЮOADCНЛХзЮяЯпгкЕуGЃЎ
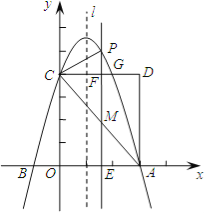
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉХзЮяЯпЕФЖдГЦжсlдкБпOAЃЈВЛАќРЈOЁЂAСНЕуЃЉЩЯЦНаавЦЖЏЃЌЗжБ№НЛxжсгкЕуEЃЌНЛCDгкЕуFЃЌНЛACгкЕуMЃЌНЛХзЮяЯпгкЕуPЃЌШєЕуMЕФКсзјБъЮЊmЃЌЧыгУКЌmЕФДњЪ§ЪНБэЪОPMЕФГЄЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНсPCЃЌдђдкCDЩЯЗНЕФХзЮяЯпВПЗжЪЧЗёДцдкетбљЕФЕуPЃЌЪЙЕУвдPЁЂCЁЂFЮЊЖЅЕуЕФШ§НЧаЮКЭЁїAEMЯрЫЦЃПШєДцдкЃЌЧѓГіДЫЪБmЕФжЕЃЌВЂжБНгХаЖЯЁїPCMЕФаЮзДЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕЅЮЛ800УћжАЙЄЛ§МЋВЮМгЯђЦЖРЇЕиЧјбЇаЃОшЪщЛюЖЏЃЌЮЊСЫНтжАЙЄЕФОшЪщЪ§СПЃЌВЩгУЫцЛњГщбљЕФЗНЗЈГщШЁ30УћжАЙЄЕФОшЪщЪ§СПзїЮЊбљБОЃЌЖдЫћУЧЕФОшЪщЪ§СПНјааЭГМЦЃЌЭГМЦНсЙћЙВга4БОЁЂ5БОЁЂ6БОЁЂ7БОЁЂ8БОЮхРрЃЌЗжБ№гУAЁЂBЁЂCЁЂDЁЂEБэЪОЃЌИљОнЭГМЦЪ§ОнЛцжЦГЩСЫШчЭМЫљЪОЕФВЛЭъећЕФЬѕаЮЭГМЦЭМЃЌ
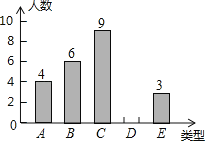
гЩЭМжаИјГіЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉЧѓет30УћжАЙЄОшЪщБОЪ§ЕФЦНОљЪ§ЃЌаДГіжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈ3ЃЉЙРМЦИУЕЅЮЛ800УћжАЙЄЙВОшЪщЖрЩйБОЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
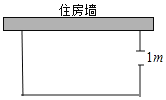
ЁОЬтФПЁПШчЭМЃЌвЛХЉЛЇвЊНЈвЛИіОиаЮжэЩсЃЌжэЩсЕФвЛБпРћгУГЄЮЊ15mЕФзЁЗПЧНЃЌСэЭтШ§БпгУ27mГЄЕФНЈжўВФСЯЮЇГЩЃЌЮЊЗНБуНјГіЃЌдкДЙжБгкзЁЗПЧНЕФвЛБпСєвЛИі1mПэЕФУХЃЌЫљЮЇОиаЮжэЩсЕФГЄЃЌПэЗжБ№ЮЊЖрЩйУзЪБЃЌжэЩсУцЛ§ЮЊ96m2ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъЙКНјСЫвЛжжаТПюаЁЕчЦїЃЌЮЊСЫбАевКЯЪЪЕФЯњЪлМлИёЃЌНјааСЫЮЊЦк5жмЕФЪдгЊЯњЃЌЪдгЊЯњЕФЧщПіШчБэЫљЪОЃК
Ек1жм | Ек2жм | Ек3жм | Ек4жм | Ек5жм | |
ЪлМл/ЃЈдЊ/ЬЈЃЉ | 50 | 40 | 60 | 55 | 45 |
ЯњЪл/ЬЈ | 360 | 420 | 300 | 330 | 390 |
вбжЊИУПюаЁЕчЦїЕФНјМлУПЬЈ30дЊЃЌЩшИУПюаЁЕчЦїУПЬЈЕФЪлМлЮЊxдЊЃЌУПжмЕФЯњСПЮЊyЬЈЃЎ
ЃЈ1ЃЉЙлВьБэжаЕФЪ§ОнЃЌЭЦЖЯyгыxТњзуЪВУДКЏЪ§ЙиЯЕЃЌВЂЧѓГіетИіКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєЯыУПжмЕФРћШѓЮЊ9000дЊЃЌдђЦфЪлМлгІЖЈЮЊЖрЩйдЊЃП
ЃЈ3ЃЉШєУПЬЈаЁЕчЦїЕФЪлМлВЛЕЭгк40дЊЃЌЕЋгжВЛФмИпгкНјМлЕФ2БЖЃЌдђШчКЮЖЈМлВХФмИќПьЕиМѕЩйПтДцЃПДЫЪБУПжмзюЖрПЩЯњЪлЖрЩйЬЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌPЪЧжБЯпyЃН2ЩЯЕФвЛИіЖЏЕуЃЌЁбPЕФАыОЖЮЊ1ЃЌжБЯпOQЧаЁбPгкЕуQЃЌдђЯпЖЮOQШЁзюаЁжЕЪБЃЌQЕуЕФзјБъЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com