【题目】下列事件为必然事件的是（ ）
A.打开电视机，播放频道正好是山西电视台
B.从一副扑克牌中任意抽出一张牌，花色是黑桃
C.买一张电影票，座位号正好是奇数
D.口袋中装有4个红球和2个白球，从中摸出3个球，其中必有红球
科目：初中数学 来源： 题型：
【题目】将四根木条钉成的长方形木框变形为平行四边形ABCD的形状，并使其面积为长方形面积的一半（木条宽度忽略不计），则这个平行四边形的最小内角为度．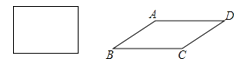
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了维护海洋权益，新组建的国家海洋局加大了在南海的巡逻力度。一天，我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻，同时发现一艘不明国籍的船只停在C处海域。如图所示，AB＝60
海里，在B处测得C在北偏东45的方向上，A处测得C在北偏西30的方向上，在海岸线AB上有一灯塔D，测得AD＝120
海里。
（1）分别求出A与C及B与C的距离AC，BC（结果保留根号）
（2）已知在灯塔D周围100海里范围内有暗礁群，我在A处海监船沿AC前往C处盘查，途中有无触礁的危险？
（参考数据：
＝1.41，
＝1.73，
＝2.45）
查看答案和解析>>
科目：初中数学 来源： 题型：
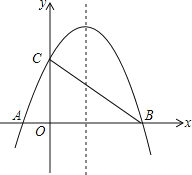
【题目】如图，已知抛物线y=﹣
+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知B点的坐标为B（8，0）．
（1）求抛物线的解析式及其对称轴方程；
（2）连接AC、BC，试判断△AOC与△COB是否相似？并说明理由；
（3）M为抛物线上BC之间的一点，N为线段BC上的一点，若MN∥y轴，求MN的最大值；
（4）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
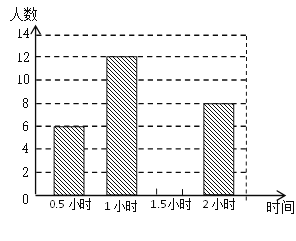
【题目】为了贯彻“减负增效”精神，掌握九年级600名学生每天的自主学习情况，某校随机抽查了九年级的部分学生，并调查他们每天自主学习的时间．根据调查结果，制作了两幅不完整的统计图如下，请根据统计图中的信息回答下列问题：
（1）此次抽样调查中，共调查了多少名学生？
（2）将图21-1补充完整；
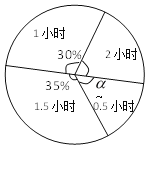
（3）求出图21-2中圆心角
的度数；
（4）请估算该校九年级学生自主学习时间不少于1.5小时的有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数： 
．
（1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
