
【题目】(1)根据下列叙述填依据:
已知:如图①,AB∥CD,∠B+∠BFE=180°,求∠B+∠BFD+∠D的度数.
解:因为∠B+∠BFE=180°,
所以AB∥EF( ).
又因为AB∥CD,
所以CD∥EF( ).
所以∠CDF+∠DFE=180°( ).
所以∠B+∠BFD+∠D=∠B+∠BFE+∠DFE+∠D=360°.
(2)根据以上解答进行探索:如图②,AB∥EF,∠BDF与∠B,∠F有何数量关系?并说明理由.
(3)如图③④,AB∥EF,你能探索出图③、图④两个图形中,∠BDF与∠B,∠F的数量关系吗?请直接写出结果.

【答案】(1)(1)同旁内角互补,两直线平行;平行于同一直线的两条直线互相平行;两直线平行,同旁内角互补;(2)∠BDF=∠B+∠F,理由见解析;(3)∠BDF=∠F-∠B.
【解析】试题分析:(1)根据平行线的性质和判定填空即可;
(2)过点D作AB的平行线DC,根据两直线平行,内错角相等证明即可;
(3)与(2)的证明方法类似,可以求出![]() 与
与![]() 的数量关系.
的数量关系.
试题解析:因为![]()
所以AB∥EF(同旁内角互补,两直线平行),
因为AB∥CD(已知),
所以CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也平行),
所以![]() (两直线平行,同旁内角互补),
(两直线平行,同旁内角互补),
所以![]()
(2)过点D作AB的平行线DC,

因为AB∥EF,
所以∠B=∠BDC,
因为AB∥EF,
所以CD∥EF,
所以∠F=∠FDC,
所以∠BDF=∠B+∠F
(3)过点D作AB的平行线DC,
根据平行线的性质可以证明图③∠BDF+∠B=∠F;图④∠BDF+∠B=∠F.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
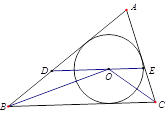
【题目】如图,⊙O是△ABC的内切圆,过点O作DE∥BC,与AB、AC分别交于点D、E.
(1)求证:BD+CE=DE;
(2)若∠BAC=70,求∠BOC的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
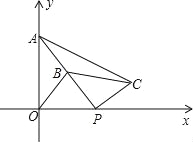
【题目】如图,在平面直角坐标系中,点A的坐标为(0,2),点P(t,0)在x轴上,B是线段PA的中点.将线段PB绕着点P顺时针方向旋转90°,得到线段PC,连结OB、BC.
(1)判断△PBC的形状,并简要说明理由;
(2)当t>0时,试问:以P、O、B、C为顶点的四边形能否为平行四边形?若能,求出相应的t的值?若不能,请说明理由;
(3)当t为何值时,△AOP与△APC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
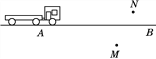
【题目】如图,M,N为坐落于公路两旁的村庄,如果一辆施工的机动车由A向B行驶,产生的噪音会对两个村庄造成影响.
(1)当施工车行驶到何处时,产生的噪音分别对两个村庄影响最大?在图中标出来.
(2)当施工车从A向B行驶时,产生的噪音对M,N两个村庄的影响情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
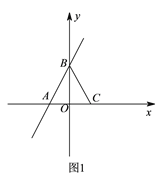
【题目】如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() .
.
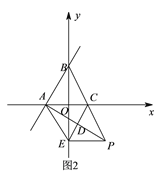
(![]() )求证:
)求证:![]() 是等边三角形.
是等边三角形.
(![]() )点
)点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() ,作
,作![]() 的垂直平分线,垂足为点
的垂直平分线,垂足为点![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,分别连接
,分别连接![]() 、
、![]() .
.
①如图![]() ,若
,若![]() ,直接写出
,直接写出![]() 的度数.
的度数.
②若点![]() 在线段
在线段![]() 的延长线上运动(
的延长线上运动(![]() 与点
与点![]() 不重合),
不重合),![]() 的度数是否变化?若变化,请说明理由;若不变,求出
的度数是否变化?若变化,请说明理由;若不变,求出![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,若点
)的条件下,若点![]() 从点
从点![]() 出发在
出发在![]() 的延长线上匀速运动,速度为每秒
的延长线上匀速运动,速度为每秒![]() 个单位长度,
个单位长度,![]() 与
与![]() 交于点
交于点![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() ,运动时间为
,运动时间为![]() 秒时.求
秒时.求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
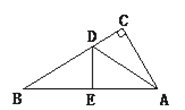
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=21,EC=9,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】附加题:
(1).填空:请用文字语言叙述勾股定理的逆定理:__________.
勾股定理的逆定理所给出的判定一个三角形是直角三角形的方法,和学过的一些其它几何图形的判定方法不同,它通过计算来判断.实际上计算在几何中也是很重要的,从数学方法这个意义上讲,我们学习勾股定理的逆定理,更重要的是拓展思维,进一步体会数学中的各种方法.
(2).阅读:小明在学习勾股定理后,尝试着利用计算的方法进行论证,解决了如下问题:
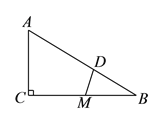
如图![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 于
于![]() ,请说明三条线段
,请说明三条线段![]() 、
、![]() 、
、![]() 总能构成一个直角三角形.
总能构成一个直角三角形.
证明:设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
消去![]() ,得
,得![]() ,从而,
,从而,![]() ,
,
又因为在![]() 中,
中,![]() ,
,
消去![]() 得
得![]() ,消去
,消去![]() ,所以
,所以![]() ,即
,即![]() .
.
所以,三条线段![]() 、
、![]() 、
、![]() 总能构成一个直角三角形.
总能构成一个直角三角形.
可见,计算在几何证明中也是很重要的.小明正是利用代数中计算、消元等手段,结合相关定理来论证了几何问题.
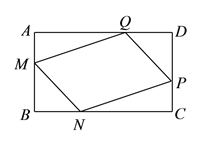
(3).解决问题:在矩形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 、
、![]() 、
、![]() 上,使得
上,使得![]() ,求证:四边形
,求证:四边形![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com