

分析 (1)根据直角三角板的直接可求得答案;
(2)由EF∥BC,可求得∠FDC的角度,可求得旋转角;过D作DG⊥EF于点G,可求得DG=$\frac{1}{2}$DF,AD=$\frac{1}{2}$BC,可得到DG=AD,可得出结论;
(3)分DF∥AB、DE∥AC和EF∥AB三种情况,可分别求得相应的旋转角.
解答 解:
(1)∵△ABC为等腰直角三角形,
∴∠B=∠C=45°,
由题可知△DEF为含30°角的三角板,
∵EF=2DE,
∴∠E=60°,∠F=30°;
(2)旋转的角度为30°,理由如下:
如图1,△ABC中,AB=AC,AD⊥BC,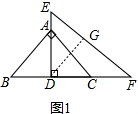
∴AD=$\frac{1}{2}$BC,
在△DEF中,过D作DG⊥EF,垂足为G,在Rt△DFG中,∠F=30°,
∴DG=$\frac{1}{2}$DF,
∵BC=DF,
∴DG=AD,
∴当EF∥BC时,点A在EF上;
(3)存在.
如图2,当DF∥AB时,则∠FDC=∠B=45°,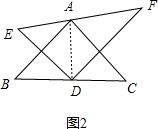
∵∠EDF=90°,
∴∠EDB=45°=∠C,
∴此时DE∥AC;
如图3,当EF∥AB时,则∠AHD=∠E=60°,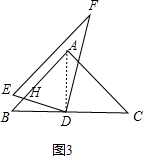
∴∠EDB=∠AHD-∠B=60°-45°=15°,
∵∠EDF=90°,
∴∠FDC=75°,
综上可知当旋转角为45°时有DE∥AC和DF∥AB,当旋转角为75°时,有EF∥AB.
点评 本题为几何变换的综合应用,涉及知识点有直角三角形的性质、旋转的性质、平行线的性质等.在(2)中利用直角三角形的性质求得AD=DG是解题的关键,在(3)中考虑平行的所有可能是解题的关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:选择题
 如图,△ABC中,将△ABC绕点A顺时针旋转40°后,得到△AB′C′,且C′在边BC上,则∠AC′C的度数为( )
如图,△ABC中,将△ABC绕点A顺时针旋转40°后,得到△AB′C′,且C′在边BC上,则∠AC′C的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小明站在自家阳台上A处观测到对面大楼底部C的俯角为α,A处到地面B处的距离AB=35m,则两栋楼之间的距离BC(单位:m)为( )
如图,小明站在自家阳台上A处观测到对面大楼底部C的俯角为α,A处到地面B处的距离AB=35m,则两栋楼之间的距离BC(单位:m)为( )| A. | 35tanα | B. | 35sinα | C. | $\frac{35}{sinα}$ | D. | $\frac{35}{tanα}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com