
����Ŀ�����壺�������������һ��������߶ΰ���������ηֳ�����С�����Σ�����һ���������ǵ��������Σ�����һ�������κ�ԭ�����ε������ڽǷֱ���ȣ���ô�����߶γ�Ϊԭ�����ε�����г�ָ����������磺��ͼ1������ֱ��������б���ϵ����߾���һ������г�ָ�����.
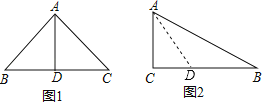
��1���жϣ��ԵĴ����̡������Ĵ���������
�ٵȱ������δ�������г�ָ��������� ����
���������������һ��������һ���ǵ�����������������αش�������г�ָ��������� ����
��2����ͼ2��Rt��ABC����C��90������B��30����BC��6�����ó߹滭������г�ָ�����������������г�ָ������ij��ȣ�
���𰸡���1���١����ڡ̣���2����г�ָ��ߡ��ij���Ϊ4��
��������
��1����������г�ָ������Ķ��弴���жϣ�
��2����ͼ����CAB��ƽ���ߣ�ֻҪ֤���߶�AD������г�ָ���������,������ֱ��������30������Ա���б�ߵ�һ���CD+BD=BC=6�����CD�ij��ȼ���.
��1������Ϊ���ȱ�����������һ���㣬�ָ�����������ζ���һ����С��60�㣬���������ǵȱ������Σ��ʵȱ������β����ڡ���г�ָ��ߡ�������ȷ���Ǽ����⣻
���������������һ��������һ���ǵ�������
����������αش��ڡ���г�ָ��ߡ����������£�
��ͼ���ڡ�ABC�У���ABC=2��C������ABC��ƽ���߽�AC��D.
��BDƽ�֡�ABC
���ABD=��DBC=![]() ,
,
�ߡ�ABC=2��C
���ABD=��DBC=��C��
��BD=DC����BDC����������
��ADB=��DBC+��C=2��C=��ABC.
��BDΪ��ABC�ĺ�г�ָ���.
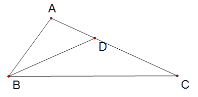
��ȷ���������⣬
�ʴ�Ϊ�������̣�
��2����ͼ2������CAB��ƽ����AD��
�ߡ�C��90�㣬��B��30�㣬
���DAB����B��30�㣬
��DA��DB��
���ADB�ǵ��������Σ��ҡ�CAD����DAB����B��
���ADC����B+��BAD����CAD+��BAD����BAC
���߶�AD�ǡ�ABC�ġ���г�ָ��ߡ���
��CD��x����BD��6��x��
��![]() ��
��
��x��2��
��AD��BD��6��2��4��
����г�ָ��ߡ��ij���Ϊ4��


 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC��һ�㣬��A=80�㣬BO��CO�ֱ�����ABC����ACB�Ľ�ƽ���ߣ�����BOC���ڣ�������

A. 140�� B. 120�� C. 130�� D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���г�Ϊ![]() ����ʣ�һ������ǽ��ǽ�������ó���Ϊ
����ʣ�һ������ǽ��ǽ�������ó���Ϊ![]() ����Χ���м����һ����ʣ�ƽ����
����Χ���м����һ����ʣ�ƽ����![]() ���ľ��λ���
���ľ��λ���![]() ���軨�Ե�һ��
���軨�Ե�һ��![]() Ϊ
Ϊ![]() ��
��
![]() ��
��![]() ________���ú�
________���ú�![]() �Ĵ���ʽ��ʾ��������
�Ĵ���ʽ��ʾ��������![]() �����
�����![]() ________���ú�
________���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
![]() ���ҪΧ�����Ϊ
���ҪΧ�����Ϊ![]() �Ļ��ԣ�
�Ļ��ԣ�![]() �ij��Ƕ��٣�
�ij��Ƕ��٣�
![]() ��
��![]() �б�ʾ����
�б�ʾ����![]() ������Ĵ���ʽͨ���䷽���ʣ���
������Ĵ���ʽͨ���䷽���ʣ���![]() ���ڶ���ʱ���ܹ�ʹ���λ���
���ڶ���ʱ���ܹ�ʹ���λ���![]() �������������Ϊ���٣�
�������������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ȱ�![]() �У���
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ�
�ϣ�![]() ����
����![]() ��
��![]() ��
��

��1����֤��![]() ��
��
��2����ͼ2���ӳ�![]() ����
����![]() ��ʹ��
��ʹ��![]() ����
����![]() �����ж�
�����ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��3���ڣ�2���������£���![]() ��
��![]() .��
.��![]() ����
����![]() ______.
______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c����A��0��2����
��1�����㣨��![]() ��0��Ҳ�ڸ��������ϣ���a��b����Ĺ�ϵʽ��
��0��Ҳ�ڸ��������ϣ���a��b����Ĺ�ϵʽ��
��2�����������������ⲻͬ����M��x1��y1����N��x2��y2�������㣺��x1��x2��0ʱ����x1��x2����y1��y2����0����0��x1��x2ʱ����x1��x2����y1��y2����0����ԭ��OΪ�ģ�OAΪ�뾶��Բ�뒁���ߵ�����������ΪB��C������ABC��һ���ڽ�Ϊ60�㣮
���������ߵĽ���ʽ��
������P���O���ڵ�A�Գƣ���O��M��N���㹲�ߣ���֤��PAƽ����MPN��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��տ������AB��EFƽ����С��ͬѧ������տ�ӱ�A�㴦����ö��ӱ�C��������տ�Ӱ��ļн���CAB=37�����غӰ�ǰ��140����B������ö�C����������տ�Ӱ��н���CBA=45��.��տ�ӵĿ���Լ������?(�ο�������sin37���0.60��cos37��=0.80��tan37��=0.75)

�鿴�𰸺ͽ���>>
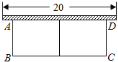
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABC�ĵױ�BC=20cm��D����AB��һ�㣬��CD=16cm��BD=12cm��

��1�����ABC��BC���ϵĸ�
��2�����ABC���ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����11���������������Ĺ㳡�и���������Ȫ������һ����ˮ�ܵ����߶�Ϊ3�ף���ʱ����ˮ�ܵ�ˮƽ����Ϊ![]() �ף�����ͼ3��ʾ������ϵ�У������Ȫ�ĺ�����ϵʽ��
�ף�����ͼ3��ʾ������ϵ�У������Ȫ�ĺ�����ϵʽ��
A. y����(x��![]() )x2��3 B. y����3(x��
)x2��3 B. y����3(x��![]() )x2��3
)x2��3
C. y����12(x��![]() )x2��3 D. y����12(x��
)x2��3 D. y����12(x��![]() )x2��3
)x2��3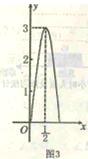
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=10��OC=8����OC����ȡһ��D����ֽƬ��AD���ۣ�ʹ��O����BC���ϵĵ�E������1����ֱ��AE�ĺ�������ʽ����2����D������꣮

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com