
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() ����
����![]() ��
��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ����ߣ���
����ߣ���![]() ���������ڵ�
���������ڵ�![]() ����
����![]() Ϊ�����߶���.
Ϊ�����߶���.
��1��ֱ��д��![]() ��������꼰
��������꼰![]() ��ֵ��
��ֵ��
��2����![]() ��������
Ϊ��������![]() ���Ϸ���һ�㣬��
���Ϸ���һ�㣬��![]() �����
�����![]() �����ꣻ
�����ꣻ
��3���ڣ�2���������£�![]() Ϊ
Ϊ![]() �����ģ���
�����ģ���![]() ����
����![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ͬʱ������2��λ/
ͬʱ������2��λ/![]() ��1��λ/
��1��λ/![]() �ٶ�������
�ٶ�������![]() ��
��![]() �������˶����˶�ʱ��Ϊ
�������˶����˶�ʱ��Ϊ![]() �루
�루![]() ��
��![]() ����ֱ��
����ֱ��![]() ����
����![]() .
.
����֤����![]() �ڶ�ֱ��
�ڶ�ֱ��![]() �ϲ���
�ϲ���![]() �Ľ���ʽ��
�Ľ���ʽ��
����![]() ��������������ֱ��
��������������ֱ��![]() �·�����
�·�����![]() ��ֱ��
��ֱ��![]() �������ʱ�����
�������ʱ�����![]() ������.
������.
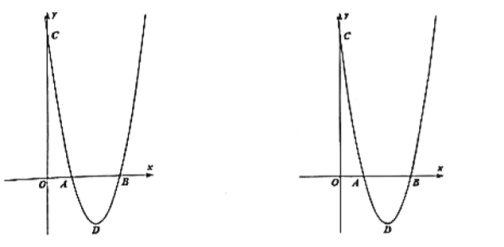
���𰸡���1��![]() ����2��
����2��![]() ����3����
����3����![]() ������������
������������![]()
��������
��1����y=0��x=0���뼴��д��![]() ��������꼰
��������꼰![]() ��ֵ��
��ֵ��
��2������![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ������
������![]() ��ã�
��ã�![]() ����ȥ����
����ȥ����![]() ���ɵ�
���ɵ�![]() .
.
��3������![]() ����
����![]() ����
����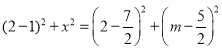 ��ã�
��ã�![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() ʱ��
ʱ��![]() �ɵ�
�ɵ�![]() ��
��![]() ʱ��ͬ������
ʱ��ͬ������![]() ����
����![]() ��ֱ��
��ֱ��![]() ��.
��.
�ڵ�![]() ��
��![]() �������ʱ�����
�������ʱ�����![]() ����
����![]() ƽ�е�ֱ�ߵĽ���ʽΪ��
ƽ�е�ֱ�ߵĽ���ʽΪ�� ![]() ����
����![]() ���ø÷�������������ȵ�ʵ�������ɵ÷���
���ø÷�������������ȵ�ʵ�������ɵ÷���![]() ��������ȵ�ʵ���������
��������ȵ�ʵ���������![]() ����
����![]() ���ɵõ�
���ɵõ�![]() ������.
������.
��1����������![]() ����
����![]() Ϊ�����߶���.
Ϊ�����߶���.
��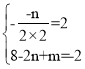
���![]()
��![]()
��y=0ʱ��![]()
���![]()
��![]()
��x=0ʱ��![]()
���![]()
��![]()
��![]()
��2����![]()
��![]()
��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]()
����ΪA��1��0��.����![]() ��ã�b=-1
��ã�b=-1
��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��![]()
��ã�![]() ����ȥ����
����ȥ����![]() ��
��
��![]() .
.
��3������![]() ��
��![]() ��
��
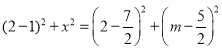
��ã�![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��![]()
��![]() ʱ��ͬ������
ʱ��ͬ������![]() ����
����![]() ��ֱ��
��ֱ��![]() ��.
��.
�ڵ�![]() ��
��![]() �������ʱ�����
�������ʱ�����![]() ����
����![]() ƽ�е�ֱ�ߵĽ���ʽΪ��
ƽ�е�ֱ�ߵĽ���ʽΪ��
![]()
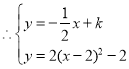 �����ȸ�
�����ȸ�
![]() �еȸ���
�еȸ���![]()
![]()


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
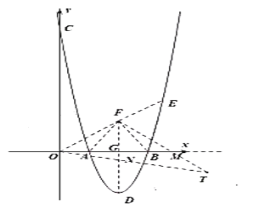
����Ŀ����ͼ��һ�κ���y��kx+b��k��bΪ������k��0����ͼ����x�ᡢy��ֱ���A��B���㣬���뷴��������y��![]() ��mΪ������m��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ����ΪD����OB��2OA��3OD��6��
��mΪ������m��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ����ΪD����OB��2OA��3OD��6��
��1����һ�κ����뷴���������Ľ���ʽ��
��2������������ͼ�����һ������E�����ꣻ
��3����۲�ͼ��ֱ��д������ʽkx+b��![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
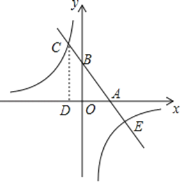
����Ŀ����ͼ�����κ���![]() ��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D������PΪy���ϵ�һ�����㣬����PD����
��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D������PΪy���ϵ�һ�����㣬����PD����![]() ����СֵΪ________.
����СֵΪ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
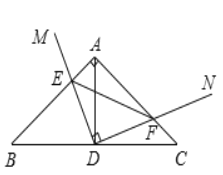
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() �Ƶ�
�Ƶ�![]() ��ת��
��ת��![]() ��
��![]() �ֱ����
�ֱ����![]() ��
��![]() ���ڡ�
���ڡ�![]() ����.���н��ۣ���
����.���н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ��
��![]() ���ܻ���ƽ��.
���ܻ���ƽ��.
���У���ȷ�Ľ�����___________________������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90����AC=8��sin A=![]()
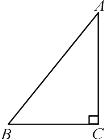
(1)��AB�ij�;
(2)����E��Rt��ABC��ֱ�DZ��ϣ���F��б��AB�ϣ�����CFE����ABCʱ����CE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������ABCD�У���DAB����B����DCB����D��90�㣬AD��BC��6��AB��CD��10����EΪ����DC�ϵ�һ�����㣬�ѡ�ADE��ֱ��AE���۵á�AD��E��
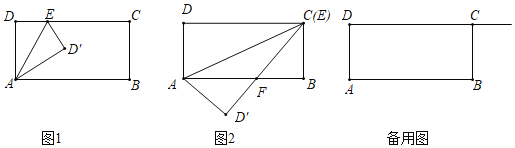
��1����D�������AB����ʱ����DAE���� ���㣻
��2����ͼ2����E����C���غ�ʱ��D��C��AB����F��
����֤��AF��FC������AF����
��3������D��B������AD��B��90��ʱ����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڵ�һԪ���η���x2+2x+k+1=0��ʵ������x1��x2��
��1����k��ȡֵ��Χ��
��2�����x1+x2��x1x2����1��kΪ��������k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������������ÿ������Ϊ40Ԫ����ߣ��г����鷢�֣�����ÿ��50Ԫ�ļ۸����ۣ�ƽ��ÿ������90��������ÿ���1Ԫ��ƽ��ÿ���������3����
(1)ƽ��ÿ���������y(��)�����ۼ�x(Ԫ/��)֮��ĺ�����ϵʽΪ�� ����
(2)���������ƽ��ÿ�����������W(Ԫ)�����ۼ�x(Ԫ/��)֮��ĺ�����ϵʽ��
(3)��۲��Ź涨ÿ���ۼ۲��ø���55Ԫ����ÿ����ߵ����ۼ�Ϊ����Ԫʱ�����Ի�����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com