
 如图,AB∥CD,EF交AB于点G,交CD与点F,FH交AB于点H,∠AGE=70°,∠BHF=125°,FH平分∠EFD吗?请说明你的理由.
如图,AB∥CD,EF交AB于点G,交CD与点F,FH交AB于点H,∠AGE=70°,∠BHF=125°,FH平分∠EFD吗?请说明你的理由.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.
如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.
如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
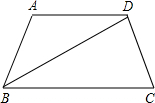 如图,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=2∠ABC,∠C=∠ABC.
如图,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=2∠ABC,∠C=∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 某市八年级学生是总体 | |
| B. | 每一名八年级学生是个体 | |
| C. | 400名八年级学生是总体的一个样本 | |
| D. | 样本容量是400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com