
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°。
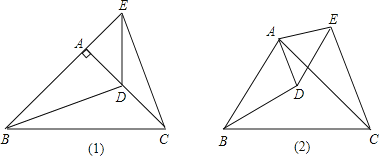
①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?写出你猜想的结论,并说明理由;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由。
【答案】①BD=CE,BD⊥CE,理由见解析;②BD=CE,BD⊥CE,理由见解析.
【解析】
试题分析:①BD=CE,BD⊥CE.根据全等三角形的判定定理SAS推知△ABD≌△ACE,然后由全等三角形的对应边相等证得BD=CE、对应角相等∠ABF=∠ECA;然后在△ABD和△CDF中,由三角形内角和定理可以求得∠CFD=90°,即BD⊥CF;②BD=CE,BD⊥CE.根据全等三角形的判定定理SAS推知△ABD≌△ACE,然后由全等三角形的对应边相等证得BD=CE、对应角相等∠ABF=∠ECA;作辅助线(延长BD交AC于F,交CE于H)BH构建对顶角∠ABF=∠HCF,再根据三角形内角和定理证得∠BHC=90°;
试题解析:解:①结论:BD=CE,BD⊥CE;理由如下:
在△ABD与△ACE中,
AB=AC,AD=AE,∠BAC=∠DAE=90°
∴△ABD≌△ACE(SAS)
∴BD=CE
如图(1),延长BD交CE于F,
∠ABD=∠ACE,∠ADB=∠CDF=∠EAC,
∴BD⊥CE
②结论:BD=CE,BD⊥CE
理由如下:∵∠BAC=∠DAE=90°
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE
在△ABD与△ACE中,
∵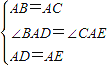
∴△ABD≌△ACE(SAS)
∴BD=CE
如图(2)延长BD交AC于F,交CE于H.
在△ABF与△HCF中,
∵∠ABF=∠HCF,∠AFB=∠HFC
∴∠CHF=∠BAF=90°
∴BD⊥CE



科目:初中数学 来源: 题型:
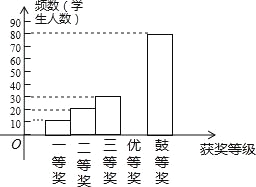
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= ,b= ,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接期中考试,小强对考试前剩余时间作了一个安排,他把计划复习重要内容的时间用一个四边形圈起来.如图,他发现,用这样的四边形圈起来五个数的和恰好是5的倍数,他又试了几个位置,都符合这样的特征。
(1)若设这五个数中间的数为a,请你用整式的加减说明其中的道理.
(2)这五个数的和能为150吗?若能,请写出中间那个数,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑车从邮局O出发,先向西骑行2km到达A村,继续向西骑行3km到达B村,然后向东骑行8km,到达C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1cm表示2km,画出数轴,并在该数轴上表示出A、B、C三个村庄的位置;
(2)C村距离A村有多远?
(3)邮递员共骑行了多少km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清代·袁牧的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )
A.8.4×10-5B.8.4×10-6C.84×10-7D.8.4×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com