
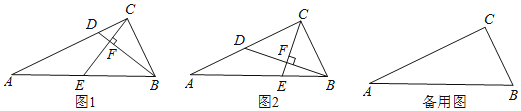
【题目】如图,Rt△ABC中,∠ACB=90°,tanA=![]() ,D、E分别在AC、AB边上,BD⊥CE于F.
,D、E分别在AC、AB边上,BD⊥CE于F.
(1)如图1,若E是AB的中点,求证:CE=BD;
(2)如图2,若![]() =
=![]() ,求tan∠ABD;
,求tan∠ABD;
(3)BC=2,P点在AC边上运动,请直接写出BP+![]() AP的最小值为 .
AP的最小值为 .
【答案】(1)证明见解析;(2)tan∠ABD=![]() ;(3)
;(3)![]()
【解析】
(1)过点E作EG⊥AC于G,先判断出AC=2BC,再判断出EG是△ABC的中位线,得出AC=2CG,进而得出BC=CG,判断出△CEG≌△BDC,即可得出结论;
(2)先判断出△CGE∽△BCD,设出CG=2m,BC=3m,进而表示出AG=4m,再用三角函数表示出EG,CD,进而表示出AD,进而借助勾股定理表示出DH,BH,即可得出结论;
(3)先作出PH=PG=![]() AP,进而得出当点B,P,H在同一条线上时,BP+PH最小,判断出AP=BP,再求出AN=PN=
AP,进而得出当点B,P,H在同一条线上时,BP+PH最小,判断出AP=BP,再求出AN=PN=![]() AB=
AB=![]() ,进而求出AP=
,进而求出AP=![]() ,即可得出结论.
,即可得出结论.
(1)证明:过点E作EG⊥AC于G,
在Rt△ABC中,tanA=![]() =
=![]() ,
,
∴AC=2BC,
∵∠ACB=90°,
∴∠GCE+∠BCE=90°,
∵BD⊥CE,
∴∠BCE+∠CBD=90°,
∴∠GCE=∠CBD,
∴∠CGE=90°=∠ACB,
∴EG∥BC,
∵点E是AB的中点,
∴EG是△ABC的中位线,
∴AC=2CG,
∴BC=CG,
∴△CEG≌△BDC(ASA),
∴CE=BD;
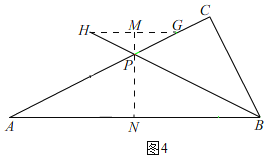
(2)如图2,由(1)知,AC=2BC,根据勾股定理得,AB=![]() BC,
BC,
过点E作EG⊥AC于G,
∴∠CGE=∠BCD=90°,
同(1)的方法得,∠ECG=∠DCB,
∴△CGE∽△BCD,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设CG=2m,BC=3m,
∴AB=3![]() m,AC=6m,
m,AC=6m,
∴AG=AC﹣CG=4m,
在Rt△AGE中,tanA=![]() =
=![]() ,
,
∴EG=![]() AG=2m,
AG=2m,
∴CD=3m,
∴AD=AC﹣CD=3m,
过点D作DH⊥AB于H,tanA=![]() =
=![]() ,
,
设DH=n,AH=2n,根据勾股定理得,![]() n=3m,
n=3m,
∴n=![]() m
m
∴DH=![]() m,AH=
m,AH=![]() m,
m,
∴BH=AB﹣AH=![]() m,
m,
在Rt△DHB中,tan∠ABD=![]() =
=![]() .
.
(3)在Rt△ABC中,tanA=![]() =
=![]() ,BC=2,
,BC=2,
∴AC=4,根据勾股定理得,AB=2![]() ,
,
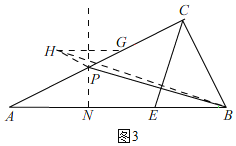
如图3,过点P作PN⊥AB交AB于N,
在AP的延长线上取一点G,使PG=![]() AP,作点G关于PN的对称点H,连接PH,此时,PH=PG=
AP,作点G关于PN的对称点H,连接PH,此时,PH=PG=![]() AP,
AP,
∴BP+![]() AP=BP+PH,
AP=BP+PH,
当点B,P,H在同一条线上时,BP+PH最小,
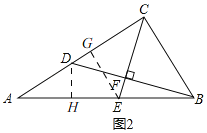
如图4,
由对性知,PH=PG,
∴∠H=∠PGH,
∵GH⊥PN,
∴HG∥AB,
∴∠A=∠PGH,∠ABP=∠H,
∴∠A=∠ABP,
∴PA=PB,
∵PN⊥AB,
∴AN=PN=![]() AB=
AB=![]() ,
,
在Rt△APN中,tanA=![]() =
=![]() ,
,
∴PN=![]() AN=
AN=![]() ,根据勾股定理得,AP=
,根据勾股定理得,AP=![]() ,
,
∴(BP+![]() AP)最小=BP+PG=BP+
AP)最小=BP+PG=BP+![]() AP=AP+
AP=AP+![]() AP=
AP=![]() AP=
AP=![]() ,
,
故答案为![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为![]() 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽量减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件,
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)当每件衬衫降价多少元时,商场每天获利最大,每天获利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
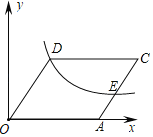
【题目】如图,在平面直角坐标系中,函数y=![]() (x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为_____.
(x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位在疫情期间用3000元购进A、B两种口罩1100个,购买A种口罩与购买B种口罩的费用相同,且A种口罩的单价是B种口罩单价的1.2倍;
(1)求A,B两种口罩的单价各是多少元?
(2)若计划用不超过7000元的资金再次购进A、B两种口罩共2600个,已知A、B两种口罩的进价不变,求A种口罩最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数![]() (a,b为常数,且
(a,b为常数,且![]() )与反比例函数
)与反比例函数![]() (m为常数,且
(m为常数,且![]() )的图象交于点A(﹣2,1)、B(1,n).
)的图象交于点A(﹣2,1)、B(1,n).

(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择.为了估计全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中的一个项目),并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
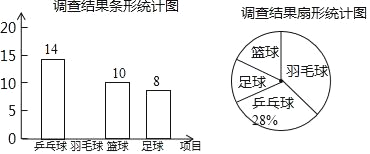
(1)求参加这次调查的学生人数,并补全条形统计图;
(2)求扇形统计图中“篮球”项目所对应扇形的圆心角度数;
(3)若该校共有600名学生,试估计该校选择“足球”项目的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实验与操作:根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)
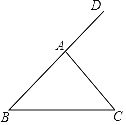
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF
探究与猜想:若∠BAE=36°,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com