
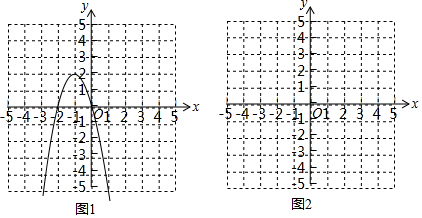
���� ��1��ֱ�ӽⷽ�̽������ú���ͼ��ó�����ʽ-2x2-4x��0�Ľ⼯��
��2�����Ȼ���y=x2-2x+1�ĺ���ͼ�������õ�y=4ʱ������x2-2x+1=4�Ľ⣬�ó�����ʽx2-2x+1��4�Ľ⼯��
��3������ax2+bx+c=0�Ľ⼯�����ú���ͼ������ó��𰸣�
��� �⣺��1���ڷ���-2x2-4x=0�Ľ�Ϊ��x1=0��x2=-2��
�۲���ʽ-2x2-4x��0�Ľ⼯Ϊ��-2��x��0��
��2���ٹ��캯��������ͼ����ͼ2����
���캯��y=x2-2x+1�������ߵĶԳ���x=1��
�ҿ������ϣ��������꣨1��0����
���ڶԳ���x=1�ԳƵ�һ�Ե㣨0��1������2��1����
�����㷨����ͼ����ͼ2��ʾ��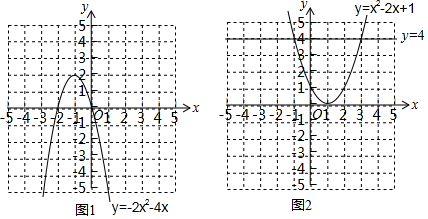 ��
��
�����ν�ϣ���ý�㣺
��y=4ʱ������x2-2x+1=4�Ľ�Ϊ��x1=-1��x2=3��
�۽���ͼ��д���⼯��
��ͼ2֪������ʽx2-2x+1��4�Ľ⼯�ǣ�-1��x��3��
��3���⣺�ٵ�b2-4ac��0ʱ������x�IJ���ʽax2+bx+c��0��a��0��
�Ľ⼯��x��$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$��x��$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$��
��b2-4ac=0ʱ������x�IJ���ʽax2+bx+c��0��a��0���Ľ⼯�ǣ�x��-$\frac{b}{2a}$��
��b2-4ac��0ʱ������x�IJ���ʽax2+bx+c��0��a��0���Ľ⼯��ȫ��ʵ����
���� ������Ҫ�����˶��κ����벻��ʽ����ȷ�������ν�Ϸ����ǽ���ؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
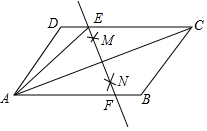 ��ƽ���ı���ABCD�У�����AC�������²�����ͼ���ֱ���A��CΪԲ�ģ��Դ���$\frac{1}{2}$AC�ij�Ϊ�뾶�����������ֱ��ཻ�ڵ�M��N����ֱ��MN��CD�ڵ�E����AB�ڵ�F����AB=6��BC=4�����ADE���ܳ�Ϊ10��
��ƽ���ı���ABCD�У�����AC�������²�����ͼ���ֱ���A��CΪԲ�ģ��Դ���$\frac{1}{2}$AC�ij�Ϊ�뾶�����������ֱ��ཻ�ڵ�M��N����ֱ��MN��CD�ڵ�E����AB�ڵ�F����AB=6��BC=4�����ADE���ܳ�Ϊ10���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
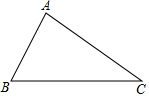 ��ͼ��ʾ���ڡ�ABC�У�
��ͼ��ʾ���ڡ�ABC�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
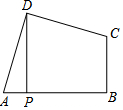 ��ͼ�������Ϊ16���ı���ABCD�У���ADC=��ABC=90�㣬AD=CD��DP��AB�ڵ�P����DP�ij���4��
��ͼ�������Ϊ16���ı���ABCD�У���ADC=��ABC=90�㣬AD=CD��DP��AB�ڵ�P����DP�ij���4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ���ı���ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����$\frac{1}{2}BF$��Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
��ͼ����ƽ���ı���ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����$\frac{1}{2}BF$��Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF�� �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
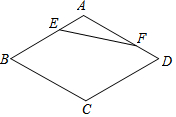 ��ͼ��������ABCD�У���B=60�㣬AB=a����E��F�ֱ��DZ�AB��AD�ϵĶ��㣬��AE+AF=a�����߶�EF����СֵΪ��������
��ͼ��������ABCD�У���B=60�㣬AB=a����E��F�ֱ��DZ�AB��AD�ϵĶ��㣬��AE+AF=a�����߶�EF����СֵΪ��������| A�� | 2$\sqrt{3}$a | B�� | $\frac{\sqrt{3}}{2}$a | C�� | $\sqrt{3}$a | D�� | $\frac{a}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com