练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    点P(1,-1)关于原点对称的点的坐标是_________.

    (-1,1) 【解析】点P(1,－1)关于原点对称的点的坐标是（－1， 1）. 故答案为（－1， 1）.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省宁波市鄞州区2017-2018学年第一学期期末考试七年级数学试卷及答案（WORD版） 题型：单选题

    下列说法正确的是（ ）

    A. 的系数是-3 B. 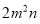的次数是2次

    C. 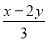是多项式 D. 的常数项是1

    C 【解析】因为单项式的系数是指单项式前数字因数,单项式的次数是指所含字母指数之和, 的系数是,所以A选项错误, 的次数是3次,所以B选项错误, 是多项式,所以C正确,因为的常数项是－1,所以D选项错误,故选C.

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市惠民县2017-2018学年七年级上学期期末数学试卷 题型：填空题

    如图，数轴上相邻刻度之间的距离是，若BC=，A点在数轴上对应的数值是-，则B点在数轴上对应的数值是 ____________．

    0或 【解析】试题解析：-+×5 =-+1 =， ∵BC=， ∴点B表示的有理数是0或． 故答案为：0或．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：解答题

    如图，已知抛物线y=- x2+bx+c与x轴交于点A（-1，0）和B，与y轴交于点C（0，3）．

    (1)求此抛物线的解析式及点B的坐标；

    (2)设抛物线的顶点为D，连接CD、DB、CB、AC．

    ①求证：△AOC∽△DCB；②在坐标轴上是否存在与原点O不重合的点P，使以P、A、C为顶点的三角形与△DCB相似？若存在，请直接写出点P的坐标；若不存在，请说明理由；

    （1）（3，0）；（2）①见解析， ② P1（9，0）或P2（0， ） 【解析】试题分析：（1）由C（0，3）得出抛物线解析式为y=－x2+bx+3，将点A的横纵坐标代入解析式求出b，令y=0，解出x即可得点B 的坐标；（2）作DE⊥y轴交于点E，不难求出∠ACB=∠DCE=45°， 则∠DCB=∠AOC=90°，由勾股定理求出CD、BC=的长度，不难发现，即可证明△AOC∽△DCB；②分情...

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：解答题

    计算：

    （1） 2cos30°－ －2 （2）(－ ) (+)

    (1)－2 (2)1 【解析】试题分析：（1）先对二次根式、三角函数值进行运算，然后进行乘法运算，最后进行减法运算即可；（2）用平方差公式将式子展开计算即可. 试题解析： （1）2cos30°－ －2=2×－×3－2=－2； （2）(－ ) (+)=3－2=1.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：单选题

    两个相似三角形的面积之比为1：9，则相似比为（ ）

    A. 1：9 B. 9：1 C. 1：3 D. 3：1

    C 【解析】两个相似三角形的面积之比为1∶9，则相似比为1∶3. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：单选题

    若直角三角形两条直角边长分别为5和12，则斜边上的中线长为（ ）

    A. 13 B. 6 C. 6.5 D. 5

    C 【解析】斜边长为： =13，所以斜边上的中线长为：6.5. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期检测八年级数学试卷 题型：单选题

    下列各式中,满足完全平方公式进行因式分解的是( )

    A. 4x2-12xy+9y2 B. 2x2+4x+1 C. 2 x2+4xy+y2 D. x2-y2+2xy

    A 【解析】试题解析：A、4x2-12xy+9y2=（2x-3y）2，能用完全平方公式进行因式分解，故此选项正确； B、2x2+4x+1，不能用完全平方公式进行因式分解，故此选项错误； C、2x2+4xy+y2，不能用完全平方公式进行因式分解，故此选项错误； D、x2-y2+2xy，不能用完全平方公式进行因式分解，故此选项错误． 故选A．

    查看答案和解析>>

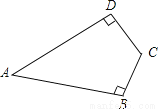
    科目：初中数学 来源：云南民族大学附属中学2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    如图， ，求证： ．

    证明见解析. 【解析】试题分析：连接AC，然后利用全等三角形的判定与性质，可得CD=CB． 试题解析：证明：连接AC，CD⊥AD，CB⊥AB，∴∠D=∠B=90°．在Rt△ADC和Rt△ABC中，∵AD=AB，AC=AC，∴Rt△ADC≌Rt△ABC（HL），∴CD=CB．

    查看答案和解析>>

    同步练习册答案