
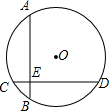
 如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,已知CE=2,ED=6,求⊙O的半径长.
如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,已知CE=2,ED=6,求⊙O的半径长. 分析 过点O分别作AB、CD的垂线OM、ON,则四边形OMEN是正方形,利用垂径定理即可求得OM,AM的长度,然后在直角△AOM中利用勾股定理即可求得OA的长度.
解答 解:过点O分别作AB、CD的垂线OM、ON,则四边形OMEN是矩形,连接OA.
∵AB=CD,AB⊥CD,
∴OM=ON,
∴矩形OMEN是正方形.
∵CE=2,ED=6,
∴CD=2+6=8,
∵ON⊥CD
∴CN=$\frac{1}{2}$CD=4,
∴EN=OM=2,
同理:AM=4.
在直角△AMO中,OA=$\sqrt{A{M}^{2}+O{M}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
∴⊙O的半径长为2$\sqrt{5}$.
点评 本题考查了垂径定理,利用垂径定理可以把求弦长以及半径的计算转化成求直角三角形的边长的计算.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定住了(AB=AC),但有工作人员说看上去有点倾斜,请你帮助工作人员测下电线杆是否倾斜,简要说明理由.
如图,电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定住了(AB=AC),但有工作人员说看上去有点倾斜,请你帮助工作人员测下电线杆是否倾斜,简要说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,在△ABC中,∠C=90°,AB=1,∠A=α,则cosα=$\frac{AC}{AB}$=AC.现在将△ABC沿AC折叠,得到△ADC,如图2,易知B,C,D三点共线,∠DAB=2α(其中0°<α<45°).
如图1,在△ABC中,∠C=90°,AB=1,∠A=α,则cosα=$\frac{AC}{AB}$=AC.现在将△ABC沿AC折叠,得到△ADC,如图2,易知B,C,D三点共线,∠DAB=2α(其中0°<α<45°).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com