
【题目】如图,矩形ABCD中,AB=6,BC=3.点E在线段BA上从B点以每秒1个单位的速度出发向A点运动,F是射线CD上一动点,在点E、F运动的过程中始终保持EF=5,且CF>BE,点P是EF的中点,连接AP.设点E运动时间为ts.



(1)在点E、F运动的过程中,AP的长度存在一个最小值,当AP的长度取得最小值时,点P的位置应该在 .
(2)当AP⊥EF时,求出此时t的值
(3)以P为圆心作⊙P,当⊙P与矩形ABCD三边所在直线都相切时,求出此时t的值,并指出此时⊙P的半径长.
【答案】(1)AD的中点;(2)t=![]() (s);(3)
(s);(3)![]() ,
,![]() ;
;![]() ,
,![]()
【解析】
(1)在点E、F运动的过程中始终保持EF=5,且CF>BE,故EF在运动过程中始终保持平行移动,因为点P是EF的中点,则点P始终在过EF的中点且平行于AB的直线上运动,运动轨迹为一条线段,在运动过程中,根据垂线段最短可得P为AD的中点时,AP的长度最小;
(2)首先过点E作EG⊥CD于点G,易证得△APE∽△EGF,然后由相似三角形的对应边成比例,求得AE的长,继而求得答案;
(3)分两种情况考虑:当⊙P在矩形ABCD内分别与AB、AD、CD相切于点Q、R、N时,连接PQ,PR,PN,如图3所示,可得出四边形AQPR和四边形RPND为两个全等的正方形,其边长为大正方形边长的一半,在直角三角形PQE中,由PE与PQ的长,利用勾股定理求出EQ的长,进而由BA+AQ-EQ求出BE的长,即为t的值,并求出此时⊙P的半径;当⊙P在矩形ABCD外分别与射线BA、AD、射线CD相切于点Q、R、N时,如图4所示,同理求出BE的长,即为t的值,并求出此时⊙P的半径.
(1)在点E、F运动的过程中始终保持EF=5,且CF>BE,故EF在运动过程中始终保持平行移动,因为点P是EF的中点,则点P始终在过EF的中点且平行于AB的直线上运动,运动轨迹为一条线段,如图所示:根据垂线段最短可得P为AD的中点时,AP的长度最小;

故答案为:AD的中点;
(2)过点E作EG⊥CD于点G,如图2
则四边形BCGE是矩形,
∴EG=BC=3,AB∥CD,
∴FG=![]() ,∠AEP=∠EFG
,∠AEP=∠EFG
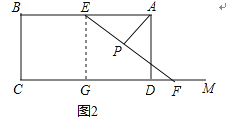
∵AP⊥EF,
∴∠APE=∠EGF=90°,
∴△APE∽△EGF,
∴ ![]()
∴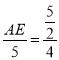
∴AE=![]()
∴BE=6-![]()
∴t=![]() (s)
(s)
(3)如图3,当⊙P在矩形ABCD内分别与AB、AD、CD相切于点Q、R、N时,
连接PQ、PR、PN,则PQ⊥AB、PR⊥AD、PN⊥CD,

则四边形AQPR与四边形RPND为两个全等的正方形,
∴PQ=AQ=AR=DR=![]() AD=
AD=![]() ,
,
在Rt△PQE中,EP=![]() ,由勾股定理可得:EQ=2,
,由勾股定理可得:EQ=2,
∴BE=BA-EQ-AQ=6-2-![]() =
=![]() ,
,
∴t=![]() ,此时⊙P的半径为
,此时⊙P的半径为![]() ;
;
如图4,当⊙P在矩形ABCD外分别与射线BA、AD、射线CD相切于点Q、R、N时,
类比图3可得,EQ=2,AQ=![]() ,
,
∴BE=BA+AQ-EQ=6+![]() -2=
-2=![]() ,
,
∴t=![]() ,此时⊙P的半径为
,此时⊙P的半径为![]() .
.


科目:初中数学 来源: 题型:
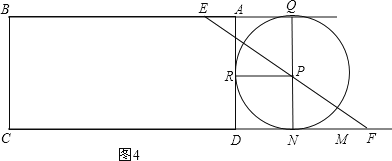
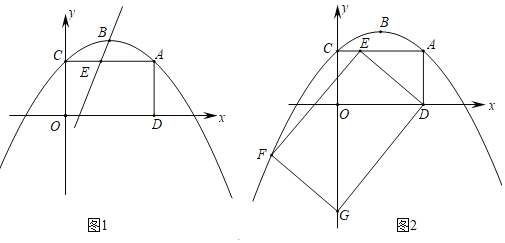
【题目】已知抛物线y=﹣![]() x2+bx+c经过点A(4,3),顶点为B,对称轴是直线x=2.
x2+bx+c经过点A(4,3),顶点为B,对称轴是直线x=2.
(1)求抛物线的函数表达式和顶点B的坐标;
(2)如图1,抛物线与y轴交于点C,连接AC,过A作AD⊥x轴于点D,E是线段AC上的动点(点E不与A,C两点重合);
(i)若直线BE将四边形ACOD分成面积比为1:3的两部分,求点E的坐标;
(ii)如图2,连接DE,作矩形DEFG,在点E的运动过程中,是否存在点G落在y轴上的同时点F恰好落在抛物线上?若存在,求出此时AE的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠C=90°,AC=6,BC=8,半径为1的⊙O与AC,BC相切,当⊙O沿边CB平移至与AB相切时,则⊙O平移的距离为( )
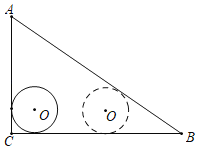
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为稳步推进5G网络建设,深化共建共享,当甲队施工20天完成5G基站建设工程的![]() 时,乙队加入该工程,结果比甲队单独施工提前25天完成了剩余的工程.
时,乙队加入该工程,结果比甲队单独施工提前25天完成了剩余的工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若乙队参与该项工程施工的时间不超过12天,则甲队从开始施工到完成该工程至少需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在“五一”假期间参加一项社会调查活动,在他所居住小区的600个家庭中,随机调查了50个家庭人均月收入情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).
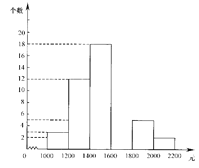
分 组 | 频 数 | 频 率 |
1000~1200 | 3 | 0.060 |
1200~1400 | 12 | 0.240 |
1400~1600 | 18 | 0.360 |
1600~1800 | 0.200 | |
1800~2000 | 5 | |
2000~2200 | 2 | 0.040 |
合计 | 50 | 1.000 |
请你根据以上提供的信息,解答下列问题:
⑴ 补全频数分布表和频数分布直方图;
⑵ 这50个家庭人均月收入的中位数落在 小组;
⑶ 请你估算该小区600个家庭中人均月收入较低(不足1400元)的家庭个数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
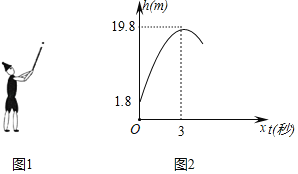
【题目】如图1,皮皮小朋友燃放一种手持烟花,这种烟花每隔2秒发射一发花弹,每一发花弹的飞行路径,爆炸时的高度均相同,皮皮小朋友发射出的第一发花弹的飞行高度![]() (米)与飞行时间
(米)与飞行时间![]() (秒)之间的函数图像如图2所示.
(秒)之间的函数图像如图2所示.
(1)求皮皮发射出的第一发花弹的飞行高度![]() (米)与飞行时间
(米)与飞行时间![]() (秒)之间的函数关系式;
(秒)之间的函数关系式;
(2)第一发花弹发射3秒后,第二发花弹达到的高度为多少米?
(3)为了安全,要求花弹爆炸时的高度不低于16米,皮皮发现在第一发花弹爆炸的同时,第二发花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(列方程解答)
(2)该车行计划今年新进一批A型车和B型车共60辆,A型车的进货价为每辆1100元,销售价与(1)相同;B型车的进货价为每辆1400元,销售价为每辆2000元,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A(-1,3),B(3,
的图象交于A(-1,3),B(3,![]() )两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
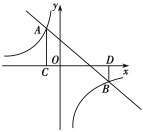
(1)求一次函数及反比例函数的解析式;
(2)若点P在直线![]() 上,且S△ACP=2S△BDP,求点P的坐标.
上,且S△ACP=2S△BDP,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com