
【题目】如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是

A、当弦PB最长时,ΔAPC是等腰三角形 B、当ΔAPC是等腰三角形时,PO⊥AC
C、当PO⊥AC时,∠ACP=300 D、当∠ACP=300时,ΔPBC是直角三角形
【答案】C。
【解析】根据圆和等边三角形的性质逐一作出判断:
当弦PB最长时,PB是⊙O的直径,所以根据等边三角形的性质,BP垂直平分AC,从而根据线段垂直平分线上的点到线段两端距离相等的性质得PA=PC,即ΔAPC是等腰三角形,判断A 正确;
当ΔAPC是等腰三角形时,根据垂径定理,得PO⊥AC,判断B正确;
当PO⊥AC时,若点P在劣弧AC上,则∠ACP=300,若点P在优弧AC上,则点P与点B重合,∠ACP=600,则∠ACP=600,判断C错误;
当∠ACP=300时,∠ABP=∠ACP=300,又∠ABC=600,从而∠PBC=300;又∠BPC=∠BAC=600,所以,∠BCP=900,即ΔPBC是直角三角形,判断D正确。
故选C。


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中∠BAC=90°,D,E分别是AB,BC的中点,F在CA的延长线上∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好落在AB边上,连接AE. 求:
(1)旋转角的度数;
(2)AE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进货价每个10元的商品按售价18元售出时,每天可卖出60个.商店经理到市场上做了一番调查后发现,若将这种商品的售价每提高1元,则日销售量就减少5个;若将这种商品的售价每降低1元,则日销售量就增加10个。为获得每日最大利润,此商品售价应定为每个多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( )

A. 30 B. 50 C. 66 D. 80
查看答案和解析>>
科目:初中数学 来源: 题型:
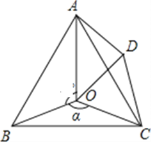
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=130°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机械租赁公司有同一型号的机械设备40套,经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出,在此基础上,当每套设备的月租金提高10元时,这种设备就少租一套,且未租出一套设备每月需要支出费用(维护费、管理费等)20元.
(1)设每套设备的月租金为![]() (元),用含
(元),用含![]() 的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
(2)租赁公司的月收益能否达到11040元?此时应该出租多少套机械设备?每套月租金是多少元?请简要说明理由;
(3)租赁公司的月收益能否在11040元基础上再提高?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com