
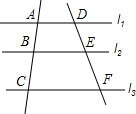 ��֪����ͼ��l1��l2��l3�����е�ʽ����$\frac{AB}{AC}$=$\frac{AD}{CF}$����$\frac{BC}{CA}$=$\frac{EF}{FD}$����$\frac{AB}{DE}$=$\frac{DF}{AC}$����$\frac{AB}{DE}$=$\frac{AD}{BE}$����AB��BC��AC=DE��EF��DF���������У�������
��֪����ͼ��l1��l2��l3�����е�ʽ����$\frac{AB}{AC}$=$\frac{AD}{CF}$����$\frac{BC}{CA}$=$\frac{EF}{FD}$����$\frac{AB}{DE}$=$\frac{DF}{AC}$����$\frac{AB}{DE}$=$\frac{AD}{BE}$����AB��BC��AC=DE��EF��DF���������У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
���� ��������ƽ���߽�����ֱ�ߣ����õĶ�Ӧ�߶γɱ����Ը���ʽ�����жϣ�
��� �⣺��l1��l2��l3��
��$\frac{AB}{AC}$=$\frac{DE}{DF}$�����Ԣٴ���
$\frac{BC}{CA}$=$\frac{EF}{FD}$�����Ԣ���ȷ��
$\frac{AB}{DE}$=$\frac{AC}{DF}$�����Ԣܴۢ���
AB��BC��AC=DE��EF��DF�����Ԣ���ȷ��
��ѡB��
���� ���⿼����ƽ���߷��߶γɱ���������ƽ���߽�����ֱ�ߣ����õĶ�Ӧ�߶γɱ�����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
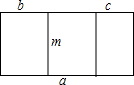 Ϊ�����̵������Ҫ�ѽ��Ļ���һ�鳤m�ף���a�ף������߷ֱ�ӿ�b��c�ף����㻭����ͼ�������ַ�����ʾ�������̵������˼�������ֱ�ʾ�����кι�ϵ��
Ϊ�����̵������Ҫ�ѽ��Ļ���һ�鳤m�ף���a�ף������߷ֱ�ӿ�b��c�ף����㻭����ͼ�������ַ�����ʾ�������̵������˼�������ֱ�ʾ�����кι�ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
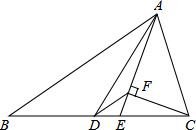 ��ͼ����ABC�У�AD�����ߣ�AE�ǽ�ƽ���ߣ�CF��AE��F��AB=5��AC=2����$\frac{AF}{EF}$=$\frac{7}{3}$��
��ͼ����ABC�У�AD�����ߣ�AE�ǽ�ƽ���ߣ�CF��AE��F��AB=5��AC=2����$\frac{AF}{EF}$=$\frac{7}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
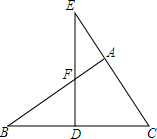 ��ͼ��ʾ���ڡ�ABC�У���BAC=90�㣬D�DZ�BC�ϵ�һ�㣬����D��ED��BC�ڵ�D����CA���ӳ����ڵ�E����AB�ڵ�F�����ҳ�ͼ�е����������Σ��������Ʒ��ű�ʾ��
��ͼ��ʾ���ڡ�ABC�У���BAC=90�㣬D�DZ�BC�ϵ�һ�㣬����D��ED��BC�ڵ�D����CA���ӳ����ڵ�E����AB�ڵ�F�����ҳ�ͼ�е����������Σ��������Ʒ��ű�ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9-x2+2xy-y2=9-��-x2-2xy+y2�� | B�� | 9-x2+2xy-y2=9-��x2-2xy-y2�� | ||
| C�� | 9-x2+2xy-y2=9-��x2-2xy+y2�� | D�� | 9-x2+2xy-y2=9+��x2-2xy+y2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
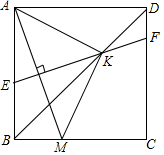 ��ͼ��������ABCD�У���M�DZ�BC��һ�㣨���ڵ�B��C����AM�Ĵ�ֱƽ���߷ֱ�AB��CD��BD��E��F��K����AK��MK��
��ͼ��������ABCD�У���M�DZ�BC��һ�㣨���ڵ�B��C����AM�Ĵ�ֱƽ���߷ֱ�AB��CD��BD��E��F��K����AK��MK���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com