
| A. | -1或3 | B. | 2 | C. | 2或3 | D. | -1 |
分析 依据二次函数的增减性分1≤h≤3、h<1、h>3三种情况,由函数的最小值列出关于h的方程,解之可得.
解答 解:∵y=-(x-h)2+3中a=-1<0,
∴当x<h时,y随x的增大而增大;当x>h时,y随x的增大而减小;
①若1≤h≤3,
则当x=1时,x=1时,函数取得最小值h,
即(1-h)2+3=h,
方程无解;
x=3时,函数取得最小值h,
即(3-h)2+3=h,
解得:h=2,h=4>3(舍去);
②若h<1,则在1≤x≤3范围内,x=3时,函数取得最小值h,
即(3-h)2+3=h,
解得:h=2>1(舍去)h=4>1(舍去);
③若h>3,则在1≤x≤3范围内,x=1时,函数取得最小值h,
即(1-h)2+3=h,
方程无解;
故选:B.
点评 本题主要考查二次函数的最值,熟练掌握分类讨论思想和二次函数的增减性是解题的关键.


科目:初中数学 来源: 题型:解答题
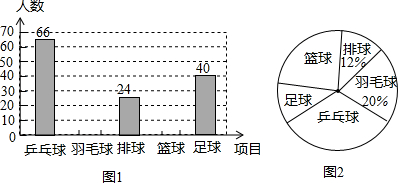
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
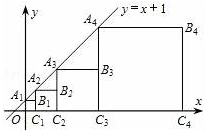 如图所示,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;然后延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;同样延长C2B2与直线y=x+1相交于点A3,再以C2A3为边作正方形C2A3B3C3,记作第三个正方形;…,依此类推,则第3个正方形的边长为4,第2017个正方形的边长为22016.
如图所示,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;然后延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;同样延长C2B2与直线y=x+1相交于点A3,再以C2A3为边作正方形C2A3B3C3,记作第三个正方形;…,依此类推,则第3个正方形的边长为4,第2017个正方形的边长为22016.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
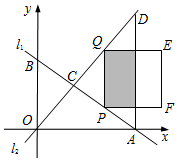 如图,直线l1与坐标轴分别交于点A、B,经过原点的直线l2与AB交于点C,与过点A且平行于y轴的直线交于点D,已知点C(3,$\frac{5}{2}$),且OA=8.在直线AB上取点P,过点P作y轴的平行线,与CD交于点Q,以PQ为边向右作正方形PQEF.设点P的横坐标为t.
如图,直线l1与坐标轴分别交于点A、B,经过原点的直线l2与AB交于点C,与过点A且平行于y轴的直线交于点D,已知点C(3,$\frac{5}{2}$),且OA=8.在直线AB上取点P,过点P作y轴的平行线,与CD交于点Q,以PQ为边向右作正方形PQEF.设点P的横坐标为t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 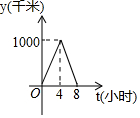 | C. |  | D. | 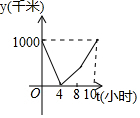 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
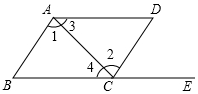 如图,点E在BC的延长线上,由下列条件能得到AD∥BC的是( )
如图,点E在BC的延长线上,由下列条件能得到AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠B=∠DCE | D. | ∠D+∠DAB=180° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com