
【题目】问题背景(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:△EFC的面积![]() __________,△ADE的面积
__________,△ADE的面积![]() ______________.
______________.
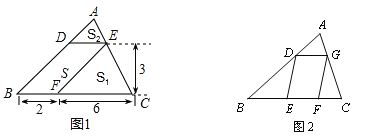
探究发现(2)在(1)中,若BF=m,FC=n,DE与BC间的距离为![]() .请证明
.请证明![]() .
.
拓展迁移(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为3、7、5,试利用(2)中的结论求△ABC的面积.
【答案】(1)![]() ,
,![]() ,
,![]() (2)
(2)![]() (3)18
(3)18
【解析】试题(1)△EFC的面积利用底×高的一半计算;△ADE的面积,可以先过点A作AH⊥BC,交DE于G,交BC于H,即AG是△ADE的高,AH是△ABC的高,利用平行线分线段成比例定理的推论,可知△ADE∽△ABC,利用相似三角形的性质可求AG,再利用三角形的面积公式计算即可;
(2)由于DE∥BC,EF∥AB,可知四边形DBFE是平行四边形,同时,利用平行线分线段成比例定理的推论,可知△ADE∽△ABC,△EFC∽△ABC,从而易得△ADE∽△EFC,利用相似三角形的面积比等于相似比的平方,可得S1:S2=n2:m2,由于S1=![]() nh,那么可求S2,从而易求4S1S2,又S=mh,容易证出结论;
nh,那么可求S2,从而易求4S1S2,又S=mh,容易证出结论;
(3)过点G作GH∥AB交BC于H,则四边形DBHG为平行四边形,容易证出△DBE≌△GHF,那么△GHC的面积等于8,再利用(2)中的结论,可求DBHG的面积,从而可求△ABC的面积.
试题解析:(1)S1=![]() ×6×3=9,
×6×3=9,
过A作AH⊥BC,交DE于G,
∵DE∥BC,EF∥AB,
∴四边形DEFB是平行四边形,
∴DE=BF=2,
∵DE∥BC,
∴AG⊥DE,△ADE∽△ABC,
∴![]() ,
,
∴![]() ,
,
解得:AG=1,
∴S2=![]() ×DE×AG=
×DE×AG=![]() =1,
=1,
(2)∵DE∥BC,EF∥AB,
∴四边形DBFE为平行四边形,∠AED=∠C,∠A=∠CEF,
∴△ADE∽△EFC,
∴![]() ,
,
∵S1=![]() nh,
nh,
∴S2=![]() ×S1=
×S1=![]() ,
,
∴4S1S2=4×![]() nh×
nh×![]() =(mh)2,
=(mh)2,
而S=mh,
∴S2=4S1S2;
(3)过点作GH∥AB交BC于H,则四边形DBHG为平行四边形,
∴∠GHC=∠B,BD=HG,DG=BH,
∵四边形DEFG为平行四边形,∴DG=EF,
∴BH=EF,
∴BE=HF,
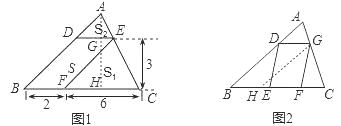
在△DBE和△GHF中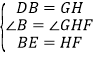 ,
,
∴△DBE≌△GHF(SAS),
∴△GHC的面积为7+5=12,
由(2)得,平行四边形DBHG的面积S为![]() =12,
=12,
∴△ABC的面积为3+12+12=27.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a<0;④b2+8a>4ac,其中正确的有( )
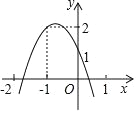
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(提出问题)如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.
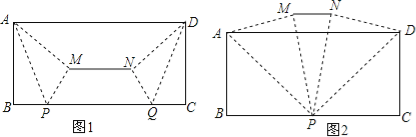
(规律探索)
(1)请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
(解决问题)
(2)如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
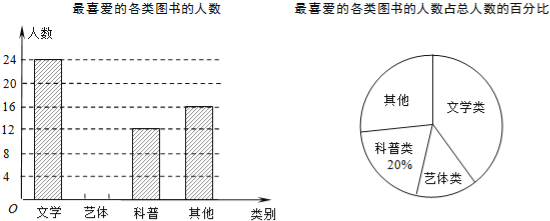
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在□ABCD中,线段EF分别交AD、AC、BC于点E、O、F,EF⊥AC,AO=CO.
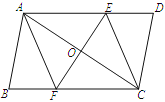
(1)求证:△AOE≌△COF;
(2)在本题的已知条件中,有一个条件如果去掉,并不影响(1)的证明,你认为这个多余的条件是 (直接写出这个条件).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织学生到市影剧院观看大型感恩歌舞剧,为了解学生如何去影剧院的问题,学校随机抽取部分学生进行调查,并将调查结果制成了表格、条形统计图和扇形统计图(均不完整).
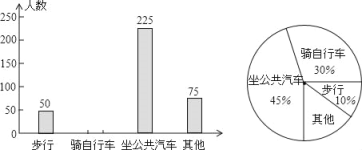
(1)此次共调查了多少位学生?
(2)将表格填充完整;
步行 | 骑自行车 | 坐公共汽车 | 其他 |
50 |
(3)将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
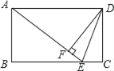
【题目】如图,在矩形ABCD中,E是BC上一点,且AE=BC,DF⊥AE,垂足是F,连接DE.
求证:(1)DF=AB;
(2)DE是∠FDC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() (点
(点![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ),射线
),射线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() .
.
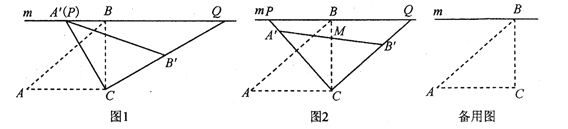
(1)如图1,当![]() 与
与![]() 重合时,求
重合时,求![]() 的度数;
的度数;
(2)如图2,设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 为
为![]() 的中点时,求线段
的中点时,求线段![]() 的长;
的长;
(3)在旋转过程中,当点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值.若存在,求出四边形
的面积是否存在最小值.若存在,求出四边形![]() 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
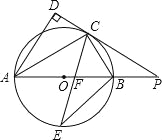
【题目】如图,AB是⊙O的直径,AC平分∠DAB交⊙O于点C,过点C的直线垂直于AD交AB的延长线于点P,弦CE交AB于点F,连接BE.
(1)求证:PD是⊙O的切线;
(2)若PC=PF,试证明CE平分∠ACB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com