
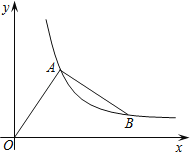
����Ŀ�������������400ǧ�ף�һ��������һ���γ��Ⱥ�Ӽس���ʻ���ҵأ���ͼ���߶�OA��ʾ������ص�·��y��ǧ�ף�������ʱ��x��Сʱ��֮��ĺ�����ϵ������BCD��ʾ�γ���ص�·��y��ǧ�ף���x��Сʱ��֮��ĺ�����ϵ������ͼ�����������⣺
��1�����߶�CD��Ӧ�ĺ�������ʽ��
��2����E������꣬������E���ʵ�����壻
��3������֪�γ��Ȼ���������20���ӣ��ҵ����ҵغ���ԭ�صȴ����������������������ͽγ����30ǧ��ʱ�����������ʱ�䣮

���㣺һ�κ�����Ӧ�ã�
���𰸡�
��������
�������:��1�����߶�CD��Ӧ�ĺ�������ʽΪy=kx+b���ɴ���ϵ���������⼴�ɣ�
��2��������ͼ���ཻ�Ľ���ָ��������������ɣ�
��3�����ɻ����ͽγ����30ǧ���г����̽�ɣ�
�⣺��1�����߶�CD��Ӧ�ĺ�������ʽΪy=kx+b��
�ɵã�![]() ��
��
��ã�![]() ��
��
�����߶�CD��Ӧ�ĺ�������ʽΪ��y=120x��140��2��x��4.5����
��2����ͼ��ɵã�ֱ��OA�Ľ���ʽΪ��y=80x��
������ͼ���ཻ�Ľ���ָ��������������
�ɵã�80x=120x��140��
��ã�x=3.5��
��x=3.5����y=80x���ã�y=280��
����E�������Ϊ��3.5��280��������ʾ����������3.5Сʱʱ�����ͽγ�������
��3�����������xh��
�ɵã�120x��140��30=80x��
��ã�x=4.25��
�ʴ�Ϊ��4.25��
��3��������֪��B��![]() ��0����
��0����
��BC�ν���ʽΪy=60x��20��![]() ��x��2����
��x��2����
���������30km�����������
1����![]() ��x��2ʱ��80x����60x��20��=30�����x=
��x��2ʱ��80x����60x��20��=30�����x=![]() ��
��
2����2��x��3.5ʱ��80x����120x��140��=30�����x=![]() ��
��
3����3.5��x��4.5ʱ��120x��140��80x=30�����x=![]() ��
��
4����4.5��x��5ʱ��400��80x=30�����x=![]() ��
��
��x=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ���ֽ���ʽx2+mx-15=��x+3����x-5������m��ֵΪ�� ��
A��-2 B��2 C��-5 D��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����4�����⣺������������( )
��1�������ε���Ǻ���180�㣻��2�������ε������ڽ���������������ǣ�
��3�����![]() ��0����ôy��0����4��ֱ��a��b��c�����a��b��b��c����ôa��c��
��0����ôy��0����4��ֱ��a��b��c�����a��b��b��c����ôa��c��
A. ��1����2�� B. ��2����3�� C. ��2����4�� D. ��3����4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ӵ����ϵĵ�A��һɽ���ϵĵ��߸�PQ����ø˶��˵�P��������45������ǰ��6m����B�㣬��ø˶��˵�P�˵˵�Q�����Ƿֱ���60����30����

��1������BPQ�Ķ�����
��2����õ��߸�PQ�ĸ߶ȣ������ȷ��1m����
�������ݣ�![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��a��b��Ϊ��һ������һ�㣬��a��b������OA�����Ե�AΪ��ת���İ�OA��ʱ��ת90������߶�BA������A��Bǡ�ö���ͬһ������������ͼ���ϣ���![]() ��ֵ���� ��
��ֵ���� ��
���㣺����������ͼ���ϵ������������������ͼ�α仯-��ת��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a + b = 5��b c = 12����a + 2b c��ֵΪ �� ��
A. 17 B. 7 C. 17 D. 7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̼����������ͬ���������������Ͼ������Ĺ������г���������д�����ʵ���㣬����̨������ij����ͷ���ѡȡ��������е��飬�����������������Ŷ��ʹ��һ�ι������г������������ε�������Ϊ���������A��ÿ�춼�ã�B������ʹ�ã�C��ż��ʹ�ã�D����δʹ�ã�����ε������������������������ͳ��ͼ��
����ͼ�е���Ϣ������������⣺
��1�����λ���� λ���������飻
��2����ȫ����ͳ��ͼ��
��3������ͳ�ƽ������������46�����������ÿ�춼�ù������г�������Լ�ж����ˣ�
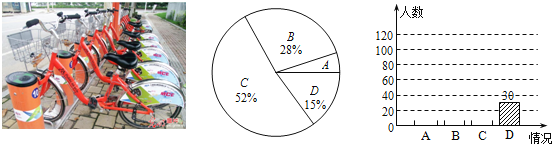
���㣺����ͳ��ͼ���������������壻����ͳ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽����
��ͼ��������y=![]() x2��
x2��![]() x��4��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
x��4��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
��1�����A��B��C�����꣮
��2������P���߶�OB���˶�ʱ��ֱ��l�ֱ�BD��BC�ڵ�M��N����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ���ʱ�����ж��ı���CQBM����״����˵�����ɣ�
��3������P���߶�EB���˶�ʱ���Ƿ���ڵ�Q��ʹ��BDQΪֱ�������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�

���㣺���κ����ۺ��⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=��k��2��x��3k2+12��
��1��kΪ��ֵʱ��ͼ��ԭ�㣻
��2��kΪ��ֵʱ��ͼ����ֱ��y=��2x+9�Ľ�����y���ϣ�
��3��kΪ��ֵʱ��ͼ��ƽ����y=��2x��ͼ��
��4��kΪ��ֵʱ��y��x�������С��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com