
 如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,点D是$\widehat{AC}$的中点,连接AC、BD交于点E,则$\frac{DE}{BE}$=( )
如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,点D是$\widehat{AC}$的中点,连接AC、BD交于点E,则$\frac{DE}{BE}$=( )| A. | $\frac{1}{5}$ | B. | $\frac{3}{16}$ | C. | 1-$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}-1}{2}$ |
分析 根据平行线的性质证得,△ADF是等腰直角三角形,求得BD=$\sqrt{2}$+1,再证△ADE∽△BDA,得ED=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1,BE=2.所以$\frac{DE}{BE}$=$\frac{\sqrt{2}-1}{2}$.
解答  解:连接AD、CD,作AF∥CD,交BE于F,
解:连接AD、CD,作AF∥CD,交BE于F,
∵点D是弧AC的中点,
∴可设AD=CD=1,
根据平行线的性质得∠AFD=∠CDF=45°.
∴△ADF是等腰直角三角形,
则AF=$\sqrt{2}$,BF=AF=$\sqrt{2}$.
∴BD=$\sqrt{2}$+1.
∵∠DAC=∠ABD,∠ADB=∠ADB,
∴△ADE∽△BDA,
∴DE=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1,BE=2.
∴$\frac{DE}{BE}$=$\frac{\sqrt{2}-1}{2}$.
点评 本题考查了圆周角定理,相似三角形的判定和性质,等腰直角三角形的判定,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C. | 2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$ | D. | 3÷$\sqrt{2}$=2$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程和时间的关系,y2表示兔子所行的路程和时间的关系,回答下列问题:
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程和时间的关系,y2表示兔子所行的路程和时间的关系,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 玉环中学学生小林从学校出发到玉环图书馆查阅资料,同时他的同学小丽刚好从玉环图书馆查完资料沿同一条路回学校.学校与玉环图书馆的路程是4千米,小林骑自行车,小丽步行,当小林沿原路回到学校时,小丽也刚好回到学校,图中折线O-A-B-C和线段DC分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
玉环中学学生小林从学校出发到玉环图书馆查阅资料,同时他的同学小丽刚好从玉环图书馆查完资料沿同一条路回学校.学校与玉环图书馆的路程是4千米,小林骑自行车,小丽步行,当小林沿原路回到学校时,小丽也刚好回到学校,图中折线O-A-B-C和线段DC分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
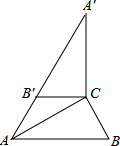 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )| A. | 6 | B. | $4\sqrt{3}$ | C. | $3\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC=4$\sqrt{5}$,sinC=$\frac{2\sqrt{5}}{5}$
如图,在△ABC中,AB=AC=4$\sqrt{5}$,sinC=$\frac{2\sqrt{5}}{5}$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 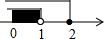 | C. | 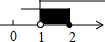 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cm | B. | 3cm | C. | 小于3cm | D. | 不大于3cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com