
| 仓库 产地 | C | D | 总计 |
| A | x吨 | 400吨 | |
| B | 300吨 | ||
| 总计 | 320吨 | 380 | 700吨 |
分析 (1)首先根据题意填表,然后由题意结合表格找到等量关系,继而求得yA,yB与x之间的函数关系式;
(2)分别从当yA=yB时,当yA>yB时,当yA<yB时去分析,利用一元一次方程与一元一次不等式的知识,即可求得答案.
解答 解:(1)
| 仓库 产地 | C | D | 总计 |
| A | x吨 | (400-x)吨 | 400吨 |
| B | (320-x)吨 | (x-20)吨 | 300吨 |
| 总计 | 320吨 | 380 | 700吨 |
点评 此题考查了一次函数的实际应用问题,考查了一次函数与一元一次方程、一元一次不等式的关系.此题难度适中,解题的关键是理解题意,找到等量关系求得函数解析式.


科目:初中数学 来源: 题型:解答题
 如图,长方形ABCD中,AB=8cm,AD=4cm,将△ABC沿着对角线AC折叠,使点B落在E处,AE交CD于F点.
如图,长方形ABCD中,AB=8cm,AD=4cm,将△ABC沿着对角线AC折叠,使点B落在E处,AE交CD于F点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
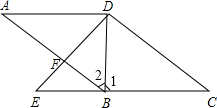 已知,如图,在四边形ABCD中,AD∥BC,点E在CB的延长线上,连接DE,交AB于点F,连接DB,且∠AFD=∠DBE,∠DBE=∠CDE.
已知,如图,在四边形ABCD中,AD∥BC,点E在CB的延长线上,连接DE,交AB于点F,连接DB,且∠AFD=∠DBE,∠DBE=∠CDE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
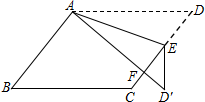 如图,在平行四边形ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=48°,∠DAE=24°,则∠FED'的大小为36°.
如图,在平行四边形ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=48°,∠DAE=24°,则∠FED'的大小为36°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在一次“寻宝”游戏中,已知寻宝图上两个标志点A(-3,0)和点B(5,0),宝藏分别埋在C(3,4)和D(-2,3)两点.请你首先建立直角坐标系确定宝藏的位置,然后在图上标出“宝藏”的位置并计算出四边形ABCD的面积.
如图所示,在一次“寻宝”游戏中,已知寻宝图上两个标志点A(-3,0)和点B(5,0),宝藏分别埋在C(3,4)和D(-2,3)两点.请你首先建立直角坐标系确定宝藏的位置,然后在图上标出“宝藏”的位置并计算出四边形ABCD的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com