
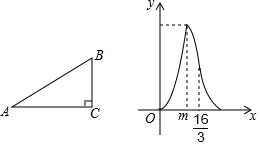
���� ��1����ȷ��ͼ����m��$\frac{16}{3}$ʱ����E��λ�ã��ٵ�E�˶���Bʱ��x=m���ڵ�H��AB��ʱ��x=$\frac{16}{3}$����ͼ1����ͼ1���֣����������������б���ʽ�ɵ�a��b�Ĺ�ϵ�����ݡ���H��AB��ʱ��x=$\frac{16}{3}$����ʽ�ɵ�a��ֵ���Ӷ���AB��ֵ������·�̳����ٶȿɵ�ʱ��m��ֵ��
��2���ٵ�0��x��4ʱ������E��AB��ʱ����ͼ2���ڵ�4��x��$\frac{16}{3}$ʱ��E��BC�ϣ�F��C�غϣ���ͼ3���۵�$\frac{16}{3}$��x��8ʱ��E��BC�ϣ���ͼ4���ֱ����������EFGH���ABC�غϲ��ֵ�������ɣ�
���  �⣺��1����E�˶���Bʱ��x=m��
�⣺��1����E�˶���Bʱ��x=m��
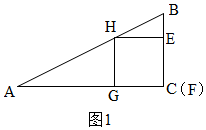
��H��AB��ʱ��x=$\frac{16}{3}$����ͼ1��
��BC=a��������EFGH�ı߳�Ϊb����AC=2a��
��HE��AC��
���BHE�ס�BAC��
��$\frac{HE}{AC}=\frac{BE}{BC}$��
��$\frac{HE}{2a}=\frac{a-b}{a}$��
��HE=b=2��a-b����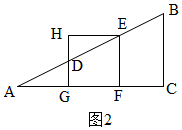
��b=$\frac{2}{3}a$��
��BE=$\frac{1}{3}$a��
�ɹ��ɶ����ã�AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{��2a��^{2}+{a}^{2}}$=$\sqrt{5}$a��
��H��AB��ʱ��E��BC�ϣ���$\frac{\sqrt{5}a}{\sqrt{5}}$+$\frac{\frac{1}{3}a}{1}$=$\frac{16}{3}$��
a=4��
��AB=4$\sqrt{5}$��
��m=$\frac{4\sqrt{5}}{\sqrt{5}}$=4��
��2���ٵ�0��x��4ʱ������E��AB��ʱ����ͼ2��
AE=$\sqrt{5}$x��
sin��A=$\frac{BC}{AB}=\frac{EF}{AE}$��
��$\frac{a}{2a}=\frac{EF}{\sqrt{5}x}$��
��EF=x��
��AF=2x��
��AG=AF-FG=2x-x=x��
��DG=$\frac{1}{2}$x��
��y=S������EFGH-S��DHE=x2-$\frac{1}{2}$$•\frac{1}{2}x•x$=$\frac{3}{4}{x}^{2}$��
�ڵ�4��x��$\frac{16}{3}$ʱ��E��BC�ϣ�F��C�غϣ���ͼ3��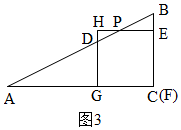
BE=x-4��
��PE=2BE=2��x-4����
EC=4-��x-4��=8-x��
��AG=AC-CG=8-��8-x��=x��
��DG=$\frac{1}{2}$x��
��DH=EC-DG=8-x-$\frac{1}{2}$x=8-$\frac{3}{2}$x��
PH=EC-PE=8-x-2��x-4��=16-3x��
��y=S������EFGH-S��DHP=��8-x��2-$\frac{1}{2}$$��8-\frac{3}{2}x����16-3x��$=-$\frac{5}{4}{x}^{2}+8x$��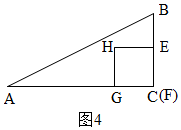
�۵�$\frac{16}{3}$��x��8ʱ��E��BC�ϣ���ͼ4��
EC=8-x��
��y=S������EFGH=��8-x��2=x2-16x+64��
����������y��x�ĺ�����ϵʽΪ��y=$\left\{\begin{array}{l}{\frac{3}{4}{x}^{2}��0��x��4��}\\{-\frac{5}{4}{x}^{2}+8x��4��x��\frac{16}{3}��}\\{{x}^{2}-16x+64��\frac{16}{3}��x��8��}\end{array}\right.$��
���� ���⿼���˶��������ͼ�����⣬����������ѣ�����ͼ����ͼ��Ĺ�ϵ�ǹؼ����ڶ��ʼ���������EFGH���ABC�غϲ��ֵ����ʱ��ע��������ۣ�����ͼ���ǹؼ���


 ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
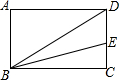 ��ͼ���ھ���ABCD�У�AB=3��BC=4������BD������CBD��ƽ���߽�CD�ڵ�E����CE�ij���Ϊ��������
��ͼ���ھ���ABCD�У�AB=3��BC=4������BD������CBD��ƽ���߽�CD�ڵ�E����CE�ij���Ϊ��������| A�� | $\frac{4}{3}$ | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
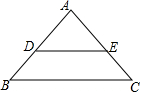 ��ͼ���ڡ�ABC�У���D��E�ֱ���AB��AC���ϣ���DE��BC����AD��DB=3��2��AE=6����EC���ڣ�������
��ͼ���ڡ�ABC�У���D��E�ֱ���AB��AC���ϣ���DE��BC����AD��DB=3��2��AE=6����EC���ڣ�������| A�� | 10 | B�� | 4 | C�� | 15 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
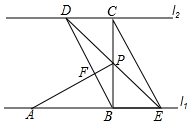 ��ͼ��ֱ��l1��l2���߶�AB��l1�ϣ�BC��l1��l2�ڵ�C����AB=BC=2cm����P�ڵ�B��C֮�䣬����P��ֱ�߷ֱ�l2��l1�ڵ�D��E����֪��CDP=45�㣮
��ͼ��ֱ��l1��l2���߶�AB��l1�ϣ�BC��l1��l2�ڵ�C����AB=BC=2cm����P�ڵ�B��C֮�䣬����P��ֱ�߷ֱ�l2��l1�ڵ�D��E����֪��CDP=45�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
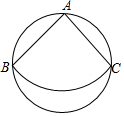 ��ͼ����һ��ֱ��Ϊ24cm��Բ��ֽƬ�ϣ�����һ��Բ�Ľ�Ϊ90�������ABC��ʹ��A��B��C����Բ���ϣ������µ�����Χ��һ��Բ�IJ��棬�����Բ�ĵ���Բ�İ뾶�ǣ�������
��ͼ����һ��ֱ��Ϊ24cm��Բ��ֽƬ�ϣ�����һ��Բ�Ľ�Ϊ90�������ABC��ʹ��A��B��C����Բ���ϣ������µ�����Χ��һ��Բ�IJ��棬�����Բ�ĵ���Բ�İ뾶�ǣ�������| A�� | 3$\sqrt{2}$cm | B�� | 2$\sqrt{3}$cm | C�� | 6cm | D�� | 12cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
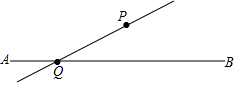 ��ͼ����Ҫ����ͼ��
��ͼ����Ҫ����ͼ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com