
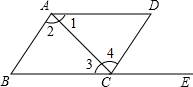
 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠1=∠3 | B. | ∠D=∠DCE | C. | ∠2=∠4 | D. | ∠D+∠BCD=180° |
分析 根据平行线的判定方法,逐项判断即可.
解答 解:A、∠1和∠3是AD、BC被AC所截得到的一对内错角,∴当∠1=∠3时,可得AD∥BC,故A不正确;
B、∠D和∠DCE是AD、BC被CD所截得到的一对内错角,∴当∠D=∠DCE时,可得AD∥BC,故B不正确;
C、∠2和∠4是AB、CD被AC所截得到的一对内错角,∴当∠2=∠4时,可得AB∥CD,故C正确;
D、∠D和∠BCD是AD、BC被CD所截得到的一对同旁内角,∴当∠D+∠BCD=180°时,可得AD∥BC,故D不正确;
故选C.
点评 本题主要考查平行线的判定,掌握平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.


科目:初中数学 来源: 题型:解答题
 如图所示,在由边长为1的25个小正方形组成的正方形网格上有一个△ABC,试在这个网格上画一个与△ABC相似,且面积最大的△A1B1C1(要求A1,B1,C1三点都在格点上).
如图所示,在由边长为1的25个小正方形组成的正方形网格上有一个△ABC,试在这个网格上画一个与△ABC相似,且面积最大的△A1B1C1(要求A1,B1,C1三点都在格点上).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数为( )| A. | 360°-4α | B. | 180°-4α | C. | α | D. | 2α-60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(4,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(4,0),点A的纵坐标是1,则点B的坐标是( )| A. | (2,1) | B. | (2,-1) | C. | (1,-2) | D. | (1,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
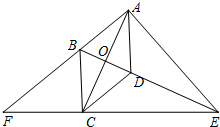 菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
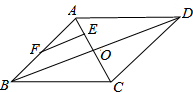 如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )
如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com