
【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为![]() 的是( )
的是( )

【答案】C.
【解析】
试题解析:A、设圆的半径是x,圆切AC于E,切BC于D,切AB于F,如图(1)同样得到正方形OECD,AE=AF,BD=BF,则a-x+b-x=c,求出x=![]() ,故本选项错误;
,故本选项错误;
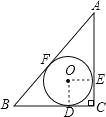
B、设圆切AB于F,圆的半径是y,连接OF,如图(2),
则△BCA∽△OFA,
∴![]() ,
,
∴![]() ,解得:y=
,解得:y=![]() ,故本选项错误;
,故本选项错误;
C、连接OE、OD,
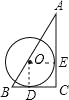
∵AC、BC分别切圆O于E、D,
∴∠OEC=∠ODC=∠C=90°,
∵OE=OD,
∴四边形OECD是正方形,
∴OE=EC=CD=OD,
设圆O的半径是r,
∵OE∥BC,∴∠AOE=∠B,
∵∠AEO=∠ODB,
∴△ODB∽△AEO,
∴![]() ,
,
![]() ,
,
解得:r=![]() ,故本选项正确;
,故本选项正确;
从上至下三个切点依次为D,E,F;并设圆的半径为x;
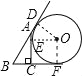
容易知道BD=BF,所以AD=BD-BA=BF-BA=a+x-c;
又∵b-x=AE=AD=a+x-c;所以x=![]() ,故本选项错误.
,故本选项错误.
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
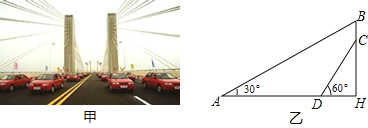
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
(1)如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE,若AC=6cm,BC=8cm,求CD的长.
(2)如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=6cm,BC=8cm,求CD的长
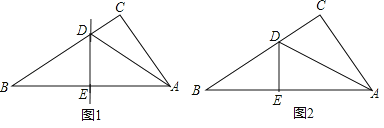
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,n个相同的因数a相乘(即) a×a×a … a记 为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3)请探究log24、log216、log264之间的数量关系_______ 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
我们知道|x|=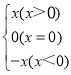 ,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x-2|时,可令x+1=0和x-2=0,分别求得x=-1,x=2(称-1,2分别为|x+1|与|x-2|的零点值),在实数范围内,零点值x=-1和x=2可将全体实数分成不重复且不遗漏的如下3种情况:
,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x-2|时,可令x+1=0和x-2=0,分别求得x=-1,x=2(称-1,2分别为|x+1|与|x-2|的零点值),在实数范围内,零点值x=-1和x=2可将全体实数分成不重复且不遗漏的如下3种情况:
(1)当x<-1时,原式=-(x+1)-(x-2)=-2x+1;
(2)当-1≤x<2时,原式=x+1-(x-2)=3;
(3)当x≥2时,原式=x+1+x-2=2x-1.综上所述,原式=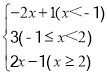
学以致用:
(Ⅰ)分别求出|x+3|和|x-1|的零点值;
(Ⅱ)化简代数式|x+3|+|x-1|;
拓展应用:
(Ⅲ)求函数y=|x+3|+|x-1|(-3≤x≤3)的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com