练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    26、我们把能平分四边形面积的直线称为“等积线”．利用如图所示的作图，可以得到四边形的“等积线”：如图1，在四边形ABCD中，取对角线BD的中点O，连接OA、OC．显然，折线AOC能平分四边形ABCD的面积，再过点O作OE∥AC交CD于E，则直线AE即为一条“等积线”．
    （1）在图1中，画出经过C点的四边形ABCD的“等积线”；
    （2）如图2，AE为四边形ABCD的一条“等积线”，F为AD边上的一点，请画出经过F点的四边形ABCD的“等积线”，并写出画图步骤．
    分析：（1）延长EO交AD于点K，连接CK．CK即为所求直线；
    （2）根据两条平行线间的距离相等，只需借助平行线即可作出经过F点的四边形ABCD的“等积线”．
    解答：解：（1）作图如下：

    （2）作图如下：①连接EF②过A作AP∥EF交CD于P③连接FP，FP即为所求直线．（8分）
    点评：本题考查了三角形的面积，能够根据两条平行线间的距离相等发现三角形的面积相等，理解“等积线”的概念．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    25、我们把能平分四边形面积的直线称为“好线”．利用下面的作图，可以得到四边形的“好线”：在四边形ABCD中，取对角线BD的中点O，连接OA、OC．显然，折线AOC能平分四边形ABCD的面积，再过点O作OE∥AC交CD于E，则直线AE即为一条“好线”．

    （1）试说明直线AE是“好线”的理由；
    （2）如下图，AE为一条“好线”，F为AD边上的一点，请作出经过F点的“好线”，并对画图作适当说明（不需要说明理由）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    我们把能平分四边形面积的直线称为“好线”．利用下面的作图，可以得到四边形的“好线”：
    （1）如图（1），在四边形ABCD中，BD为其中一条对角线，请你用尺规作图的方法找出BD的中点O；
    （2）如图（2），在四边形ABCD中，对角线BD的中点为O，连结OA、OC．显然，折线AOC能平分四边形ABCD的面积，再过点O作OE∥AC交CD于E，则直线AE即为一条“好线”．试说明直线AE是“好线”的理由；
    （3）如图（3），AE为四边形ABCD一条“好线”，F为AD边上的一点，请作出经过F点的“好线”，并对画图作适当说明（不需要说明理由）．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江苏省崇安区七年级下学期期中考试数学卷（带解析） 题型：解答题

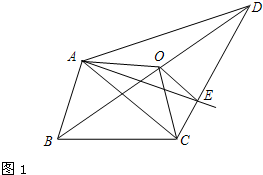
    我们把能平分四边形面积的直线称为“好线”.利用下面的作图，可以得到四边形的“好线”：如图1，在四边形ABCD中，取对角线BD的中点O，连结OA、OC. 显然，折线AOC能平分四边形ABCD的面积，再过点O作OE∥AC交CD于E，则直线AE即为一条“好线”.

    （1）试说明直线AE是“好线”的理由；
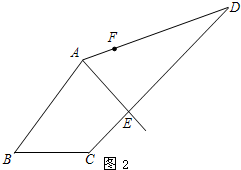
    （2）如图2，AE为一条“好线”，F为AD边上的一点，请作出经过F点的“好线”，只需对画图步骤作适当说明（不需要说明“好线”的理由）.

    查看答案和解析>>

    科目：初中数学 来源：2014届江苏省崇安区七年级下学期期中考试数学卷（解析版） 题型：解答题

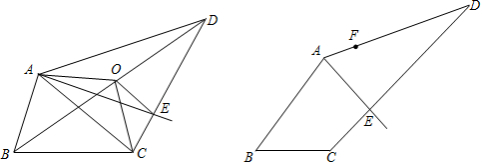
    我们把能平分四边形面积的直线称为“好线”.利用下面的作图，可以得到四边形的“好线”：如图1，在四边形ABCD中，取对角线BD的中点O，连结OA、OC. 显然，折线AOC能平分四边形ABCD的面积，再过点O作OE∥AC交CD于E，则直线AE即为一条“好线”.

    （1）试说明直线AE是“好线”的理由；

    （2）如图2，AE为一条“好线”，F为AD边上的一点，请作出经过F点的“好线”，只需对画图步骤作适当说明（不需要说明“好线”的理由）.

     

    查看答案和解析>>

    同步练习册答案