
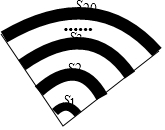
 手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1,若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=205π.
手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1,若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=205π. 分析 由图可知S1=$\frac{1+2}{4}$π,S2=$\frac{3+4}{4}$π,S3=$\frac{5+6}{4}$π,…,Sn=$\frac{4n-1}{4}$π,再根据等差数列求和公式可求S1+S2+S3+…+S20的值.
解答 解:依题意有:
S1=$\frac{1+2}{4}$π,
S2=$\frac{3+4}{4}$π,
S3=$\frac{5+6}{4}$π,
…,
S20=$\frac{39+40}{4}$π,
则S1+S2+S3+…+S20=$\frac{1+2+3+4+…+39+40}{4}$π=205π.
故答案为:205π.
点评 考查了扇形面积的计算,本题是一道规律性的题目,难度较大.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x5•x5=x10 | B. | x5+x5=2x5 | ||
| C. | (-x5)5=-x25 | D. | (2x2y)3÷($\frac{1}{4}$xy3)=$\frac{1}{2}$x5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,△ABC中,AB=AC,∠BAC=45°,过C作CF∥AB,过A,B分别向直线CF作垂线,垂足分别为F,E,过B作BG⊥AC于G.
已知,△ABC中,AB=AC,∠BAC=45°,过C作CF∥AB,过A,B分别向直线CF作垂线,垂足分别为F,E,过B作BG⊥AC于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com