13.我们称A=$|\begin{array}{l}{{a}_{11}}&{{a}_{12}}&{…}&{{a}_{1m}}\\{{a}_{21}}&{{a}_{22}}&{…}&{{a}_{2n}}\\{…}&{…}&{…}&{…}\\{{a}_{m1}}&{{a}_{n2}}&{…}&{{a}_{mn}}\end{array}|$为一个m×n的矩阵,下标ij表示元素a7位于该矩阵的第i行、第j列.矩阵乘法满足如下规则:
C=A×B=$|\begin{array}{l}{{a}_{11}}&{{a}_{12}}&{…}&{{a}_{1n}}\\{{a}_{21}}&{{a}_{22}}&{…}&{{a}_{2n}}\\{…}&{…}&{…}&{…}\\{{a}_{n1}}&{{a}_{m2}}&{…}&{{a}_{mn}}\end{array}|$×$|\begin{array}{l}{{b}_{11}}&{{b}_{12}}&{…}&{{b}_{1n}}\\{{b}_{21}}&{{b}_{22}}&{…}&{{b}_{2n}}\\{…}&{…}&{..}&{…}\\{{b}_{n1}}&{{b}_{b2}}&{…}&{{b}_{mn}}\end{array}|$=$|\begin{array}{l}{{c}_{11}}&{{c}_{12}}&{…}&{{c}_{1n}}\\{{c}_{21}}&{{c}_{22}}&{…}&{{c}_{2n}}\\{…}&{…}&{…}&{…}\\{{c}_{m1}}&{{c}_{n2}}&{…}&{{c}_{mn}}\end{array}|$
其中CB=au×bu+a12×b2j+…+ay×by
比如:$(\begin{array}{l}{1}&{2}\\{3}&{4}\end{array})$×$(\begin{array}{l}{5}&{6}\\{7}&{8}\end{array})$=$(\begin{array}{l}{1×5+2×7}&{1×6+2×8}\\{3×5+4×7}&{3×6+4×8}\end{array})$=$(\begin{array}{l}{19}&{22}\\{43}&{50}\end{array})$
那么,请你计算$(\begin{array}{l}{1}&{1}&{-2}\\{-2}&{-2}&{4}\end{array})$×$(\begin{array}{l}{1}&{2}\\{-1}&{0}\\{0}&{1}\end{array})$=$(\begin{array}{l}{0}&{0}\\{0}&{0}\end{array})$.
分析 原式利用题中的新定义计算即可得到结果.
解答 解:根据题中的新定义得:原式=$(\begin{array}{l}{1-1+0}&{2+0-2}\\{-2+2+0}&{-4+0+4}\end{array})$=$(\begin{array}{l}{0}&{0}\\{0}&{0}\end{array})$.
故答案为:$(\begin{array}{l}{0}&{0}\\{0}&{0}\end{array})$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).画出△ABC关于y轴对称的△A1B1C1,并写出点A1、B1、C1的坐标.
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).画出△ABC关于y轴对称的△A1B1C1,并写出点A1、B1、C1的坐标.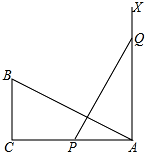 如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP=6或12.
如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP=6或12.