
分析 (1)首先将mn+2m-n=6变形为(m-1)(n+2)=4,从而推出“友好点”都在反比例函数y=$\frac{4}{x}$图象上,由此列出方程即可解决问题.
(2)首先判断点A、B在第一象限,且关于直线y=x对称,由此可知A(a,b),B(b,a),利用待定系数法即可解决问题.
解答 解:(1)由mn+2m-n=6得:mn+2m-n-2=4,
∴(m-1)(n+2)=4,
∵点(m-1,n+2)为“友好点”,
所以“友好点”都在反比例函数y=$\frac{4}{x}$图象上,
∵(1,y2)是“友好点”,
∴1•y2=4,
∴y=±2,
经检验,y=±2时,(1,y2)是“友好点”.
(2)∵点A和点B是两个不同的“友好点”,它们的横坐标分别是a和b,且OA2=OB2,
∴根据“友好点”的定义可知A、B在第一象限,且关于直线y=x对称.
∴A(a,b),B(b,a),
∵$\frac{1}{2}$≤a≤2,A、B在反比例函数y=$\frac{4}{x}$上,
∴当a=$\frac{1}{2}$时,b=8,当a=2时,b=2,
∴2≤b≤8.
点评 本题主要考查的是反比例函数和正比例函数的应用,解题的关键是发现“友好点”都在反比例函数y=$\frac{4}{x}$图象上,根据OA2=OB2,推出A、B关于直线y=x对称,题目有一定的难度,学会用转化的思想思考问题,属于中考创新题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
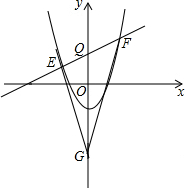 如图,抛物线y=$\frac{1}{2}$x2-2交y轴于C,不平行于x轴的直线y=kx+3交抛物线于E、F,交y轴于点Q,在y轴的负半轴上是否存在点G使EQ•FG=FQ•EG,若存在,请求出G点坐标;若不存在.请说明理由.
如图,抛物线y=$\frac{1}{2}$x2-2交y轴于C,不平行于x轴的直线y=kx+3交抛物线于E、F,交y轴于点Q,在y轴的负半轴上是否存在点G使EQ•FG=FQ•EG,若存在,请求出G点坐标;若不存在.请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com