
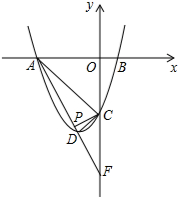
 如图,已知抛物线y=ax2+bx+c与x轴交于点A、B(2,0),与直线AC:y=-x-6交y轴于点C,点D是抛物线的顶点.
如图,已知抛物线y=ax2+bx+c与x轴交于点A、B(2,0),与直线AC:y=-x-6交y轴于点C,点D是抛物线的顶点.分析 (1)根据自变量与函数值的对应关系,可得A、C点坐标,根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)根据勾股定理及逆定理,可得三角形的形状,根据正切值等对边比邻边,可得答案;
(3)根据待定系数法,可得AD的解析式,根据等式的性质,可得∠DFC=∠PCD,根据相似三角形的判定与性质,可得关于x的方程,根据自变量与函数值的对应关系,可得答案.
解答 解:(1)直线AC:y=-x-6,
当x=0时,y=-6,即C(0,-6).
当y=0时,x=-6,即A(-6,0).
∵B(2,0),
把A、B、C三点坐标代入函数解析式,得
$\left\{\begin{array}{l}{36a-6b+c=0}\\{4a+2b+c=0}\\{c=-6}\end{array}\right.$,解得
$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=2}\\{c=-6}\end{array}\right.$,
抛物线的解析式为y=$\frac{1}{2}$x2+2x-6=$\frac{1}{2}$(x+2)2-8,
顶点D的坐标为(-2,-8);
(2)△ACD是直角三角形,理由如下:
∵A(6,0),C(0,-6),D(-2,-8),
∴由勾股定理,得AC2=62+62=72,CD2=22+(-8+6)2=8,AD2=(-2+6)2+82=80,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,∠ACD=90°
∴tan∠ADC=$\frac{AC}{CD}$=$\frac{6\sqrt{2}}{2\sqrt{2}}$=3;
(3)设直线AD的解析式为y=mx+n.
∵A(-6,0),D(-2,-8),
$\left\{\begin{array}{l}{-6m+n=0}\\{-2m+n=-8}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-2}\\{n=-12}\end{array}\right.$,
∴直线AD的解析式为y=-2x-12.
当x=0时,y=-12,即F(0,-12),
设点P的坐标为(x,-2x-12).
∵∠ADC=∠DCF+∠DFC,∠PCF=∠DCF+∠PCD,∠ADC=∠PCF,
∴∠DFC=∠PCD,
在△CPD和△FPC中,$\left\{\begin{array}{l}{∠PCD=∠PFC}\\{∠CPD=∠FPC}\end{array}\right.$,
∴△CPD∽△FPC,
∴$\frac{CP}{FP}$=$\frac{CD}{FC}$,
∴$\frac{{x}^{2}+(-2x-12+6)^{2}}{{x}^{2}+(2x)^{2}}$=$\frac{8}{{6}^{2}}$,化简,得
35x2+216x+324=0,
解得x1=-$\frac{18}{7}$,x2=-$\frac{18}{5}$(舍去).
当x=-$\frac{18}{7}$时,-2x-12=-2×(-$\frac{18}{7}$)-12=-$\frac{48}{7}$,
∴点P的坐标(-$\frac{18}{7}$,-$\frac{48}{7}$).
点评 本题考查了二次函数综合题,利用待定系数是求函数解析式得关键;(2)利用勾股定理及逆定理是解题关键;(3)利用相似三角形的判定与性质得出关于x的方程是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 8 | C. | 6或10 | D. | 8或10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形
已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 端午节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,顾客就可以分别获得玩具熊、童话书、水彩笔.小明和妈妈购买了125元的商品,请你分析计算:
端午节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,顾客就可以分别获得玩具熊、童话书、水彩笔.小明和妈妈购买了125元的商品,请你分析计算:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com