

���� ��1�����ݶ�����Ϊ����ʽ�������ʽ���ɣ�
��2�����������ȣ�������ߣ�����������������ƽ���ߣ������Գ����㼴�ɣ�
��3������ͼ�Σ���㣬�������ƽ���������ϵ��⼴�ɣ�
��� �⣺��ͼ1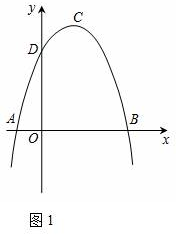
��1�������������ߵĽ���ʽΪ��y=a��x-1��2+4��
�����⣬����B��3��0�����룬�ã�a��3-1��2+4=0��
��ã�a=-1��
�����������ߵĽ���ʽΪ��y=-��x-1��2+4=-x2+2x+3
�൱y=0ʱ��-��x-1��2+4=0��
��x=-1��x=3��
���A��-1��0����
��2����GΪ��֪�����ߵĶԳ����ϵ�����һ�㣬����BGD��������ڡ�ADB�����ʱ�����G�����ꣻ
��ͼ2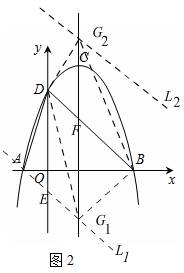
��y=-��x-1��2+4 ֪�Գ���Ϊx=1��
��y=-��x-1��2+4��
�У���x=0����y=3���D������Ϊ��0��3����
��ֱ��BD�Ľ���ʽΪy=kx+b��
��B��3��0����D��0��3��������룬�ã�$\left\{\begin{array}{l}{0=3k+b}\\{3=b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$��
��ֱ��BD�Ľ���ʽΪy=-x+3��
��Rt��BOD��DB=$\sqrt{{3^2}+{3^2}}=3\sqrt{2}$��
�֡�${S_{��ADB}}=\frac{1}{2}AB•OD=\frac{1}{2}��4��3$=6��
���ABD��BD���ϵĸ�Ϊh��
����$\frac{1}{2}BD•h=6$����$\frac{1}{2}��3\sqrt{2}h=6$��
��$h=2\sqrt{2}$��
������ƽ������ֱ��ƽ����BD���ҵ�BD�ľ������$h=2\sqrt{2}$��
������ֱ�����������ֱ�ΪL1��L2����ֱ����Գ���x=1��
����������G1��G2��������ĵ㣬
��L1��y�ύ�ڵ�E��BD��ֱ��x=1���ڵ�F������֪������֪�ı���DEG1FΪƽ���ı��Σ�
��DE=FG1��
��Rt��DOB��Rt��EOA��OD=OB��
���ODB=45�㣬���OEA=45��
��OE=OA=1��DE=4��
�ཫֱ��BD����ƽ��4����λ��ΪL1��y=-x-1��
ͬ������ֱ��BD����ƽ��4����λ��ΪL2��y=-x+7��
������$\left\{\begin{array}{l}{y=-x-1}\\{x=1}\end{array}\right.$����ã�$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$��
����$\left\{\begin{array}{l}{y=-x-7}\\{x=1}\end{array}\right.$����ã�$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$��
��G1��1��-2��G2��1��6����
��3����ͼ3��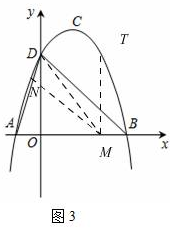
�������֪����NMD=��MDB��Ҫʹ����DNM�ס�BMD��ֻҪʹ$\frac{NM}{MD}=\frac{MD}{BD}$���ɣ�
����MD2=NM��BD��
���M��������a��0������MN��BD��
�ɵá�AMN�ס�ABD��
��$\frac{NM}{BD}=\frac{AM}{AB}$��
���ɣ�1������2����֪��AM=1+a��BD=$3\sqrt{2}$��AB=4��
��$MN=\frac{AM��BD}{AB}=\frac{{��1+a����3\sqrt{2}}}{4}=\frac{{3\sqrt{2}}}{4}��1+a��$��
��MD2=OD2+OM2=a2+9��
��${a^2}+9=\frac{{3\sqrt{2}}}{4}��1+a����3\sqrt{2}$��
��ã�$a=\frac{3}{2}$��a=3���������⣬��ȥ����
���M��������$\frac{3}{2}$��0����
�֡ߵ�T��������y=-��x-1��2+4ͼ���ϣ�
�൱x=$\frac{3}{2}$ʱ��y=$\frac{15}{4}$��
���T��������$\frac{3}{2}$��$\frac{15}{4}$����
���� ������Ҫ������κ������ۺ����⣬���ö���ʽ�������ߣ�����������Ƚ���ƽ���߽��⣬��������ƽ�����ϵ��ֵ�ǽ���Ĺؼ���


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ���ڱ���ȵľ����������� | |
| B�� | �Խ����ഹֱ��ƽ���ı��������� | |
| C�� | �������εĶԽǺ���� | |
| D�� | ���εĶԽ����ഹֱƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������ֽƬABCD�ı��ǡ�O�뾶��4������O��������ABCD�����ģ���ֽƬ����ͼʾ��ʽ�۵���ʹEA1ǡ�����0�����ڵ�A1����tan��A1EF��ֵΪ$\frac{2}{3}$��
��ͼ����֪������ֽƬABCD�ı��ǡ�O�뾶��4������O��������ABCD�����ģ���ֽƬ����ͼʾ��ʽ�۵���ʹEA1ǡ�����0�����ڵ�A1����tan��A1EF��ֵΪ$\frac{2}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ���ڡ�ABC�У�AB=AC��AD�ǡ�ABC��һ����ƽ���ߣ�AN�ǡ�ABC��ǡ�CAM��ƽ���ߣ�CE��AN������Ϊ��E��
��֪����ͼ���ڡ�ABC�У�AB=AC��AD�ǡ�ABC��һ����ƽ���ߣ�AN�ǡ�ABC��ǡ�CAM��ƽ���ߣ�CE��AN������Ϊ��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{1.44}$=��1.2 | B�� | $\sqrt{��\frac{9}{4}��^{2}}$=$\frac{3}{2}$ | C�� | $\sqrt{��-2��^{2}}$=-2 | D�� | $\sqrt{\frac{49}{25}}$=$\frac{7}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 3$-\sqrt{5}$ | C�� | $\frac{1}{2}$��3$-\sqrt{5}$�� | D�� | 1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com