
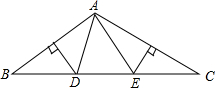
 如图,在△ABC中,AB边垂直平分线交BC于点D,AC边垂直平分线交BC于点E,连接AD,AE.
如图,在△ABC中,AB边垂直平分线交BC于点D,AC边垂直平分线交BC于点E,连接AD,AE.分析 (1)根据线段的垂直平分线的性质得到DB=DA,EC=EA,根据等腰三角形的性质解答即可;
(2)分两种情况进行讨论,先根据线段垂直平分线的性质,得到∠B=∠BAD,∠C=∠CAE,进而得到∠BAD+∠CAE=∠B+∠C=180°-α,再根据角的和差关系进行计算即可.
解答 解:(1)∵AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,
∴DB=DA,EC=EA,
∵∠BAC=110°,
∴∠B+∠C=70°,
∵DB=DA,EC=EA,
∴∠DAB=∠B,∠EAC=∠C,
∴∠DAB+∠EAC=70°,
∴∠DAE=110°-70°=40°,
(2)分两种情况:
①如图所示,当∠BAC≥90°时,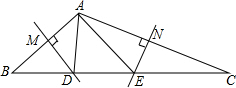
∵DM垂直平分AB,
∴DA=DB,
∴∠B=∠BAD,
同理可得,∠C=∠CAE,
∴∠BAD+∠CAE=∠B+∠C=180°-θ,
∴∠DAE=∠BAC-(∠BAD+∠CAE)=θ-(180°-θ)=2θ-180°;
②如图所示,当∠BAC<90°时,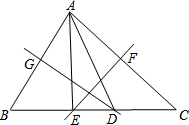
∵DM垂直平分AB,
∴DA=DB,
∴∠B=∠BAD,
同理可得,∠C=∠CAE,
∴∠BAD+∠CAE=∠B+∠C=180°-θ,
∴∠DAE=∠BAD+∠CAE-∠BAC=180°-θ-θ=180°-2θ.
点评 本题考查了三角形内角和定理,线段垂直平分线性质的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
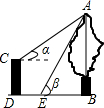 学习完解直角三角形知识,同学们利用它求我校某平房前一棵大树的高度,如图,大树AB与平房CD底部在同一平地,知道二层平房CD高为6米,在平房顶部点C测得树顶A点的仰角α=30°,从平房底部向树的方向水平前进2米到达点E,在点E处测得大树顶A的仰角β=60°,请你帮同学们求出这棵大树高度AB(结果保留根号)
学习完解直角三角形知识,同学们利用它求我校某平房前一棵大树的高度,如图,大树AB与平房CD底部在同一平地,知道二层平房CD高为6米,在平房顶部点C测得树顶A点的仰角α=30°,从平房底部向树的方向水平前进2米到达点E,在点E处测得大树顶A的仰角β=60°,请你帮同学们求出这棵大树高度AB(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 22017 | B. | -1 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{11}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{20}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com