
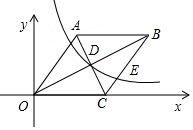
 如图,菱形OABC的边OC在x轴正半轴上,点B的坐标为(8,4).
如图,菱形OABC的边OC在x轴正半轴上,点B的坐标为(8,4).分析 (1)过B作BM⊥x轴于点M,根据B的坐标求出BM=4,在Rt△BCM中,根据勾股定理得出方程,求出方程的解即可;
(2)求出反比例函数解析式,求出直线BC,求出直线BC和反比例函数的交点坐标,即可得出答案.
解答 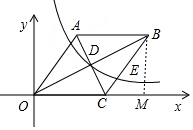 解:(1)如图,BM⊥x轴于点M,
解:(1)如图,BM⊥x轴于点M,
∵点B的坐标为(8,4),OC=BC,
∴CM=8-BC,
在Rt△BCM中,BC2=CM2+BM2,即BC2=(8-BC)2+42,
解得,BC=5,即菱形的边长为5;
(2)∵D是OB的中点,
∴点D的坐标为:(4,2),
∵点D在反比例函数y=$\frac{k}{x}$上,
∴k=xy=4×2=8,y=$\frac{8}{x}$,
又∵OC=5,
∴C(5,0),
∴可求直线BC为y=$\frac{4}{3}$x-$\frac{20}{3}$,
令$\frac{4}{3}$x-$\frac{20}{3}$=$\frac{8}{x}$,解得x1=6,x2=-1(舍去),
当x=6时,y=$\frac{8}{6}$=$\frac{4}{3}$,
∴点E的坐标为(6,$\frac{4}{3}$).
点评 本题考查了一次函数和反比例函数的交点问题,菱形的性质,勾股定理等知识点,能根求出两函数的解析式和得出关于OC的方程是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
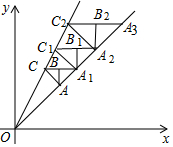 如图,在平面直角坐标系第一象限内,直线y=x与直线y=2x的内部作等腰Rt△ABC,是∠ABC=90°,边BC∥x轴,AB∥y轴,点A(1,1)在直线y=x上,点C在直线y=2x上:CB的延长线交直线y=x于点A1,作等腰Rt△A1B1C1,是∠A1B1C1=90°,B1C1∥x轴,A1B1∥y轴,点C1在直线y=2x上…按此规律,则等腰Rt△AnBnCn的腰长为$\frac{{4}^{n}}{{3}^{n+1}}$.
如图,在平面直角坐标系第一象限内,直线y=x与直线y=2x的内部作等腰Rt△ABC,是∠ABC=90°,边BC∥x轴,AB∥y轴,点A(1,1)在直线y=x上,点C在直线y=2x上:CB的延长线交直线y=x于点A1,作等腰Rt△A1B1C1,是∠A1B1C1=90°,B1C1∥x轴,A1B1∥y轴,点C1在直线y=2x上…按此规律,则等腰Rt△AnBnCn的腰长为$\frac{{4}^{n}}{{3}^{n+1}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
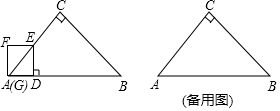
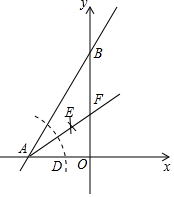 如图,在平面直角坐标系中,一次函数y=$\sqrt{3}$x+1的图象分别与x轴、y轴交于A、B两点,以A为圆心,适当长为半径画弧分别交AB、AO于点C、D,再分别以C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧交于点E,连接AE并延长交y轴于点F,则下列说法正确的个数是( )
如图,在平面直角坐标系中,一次函数y=$\sqrt{3}$x+1的图象分别与x轴、y轴交于A、B两点,以A为圆心,适当长为半径画弧分别交AB、AO于点C、D,再分别以C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧交于点E,连接AE并延长交y轴于点F,则下列说法正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
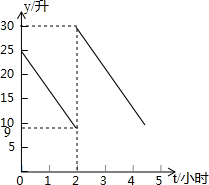 张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com