
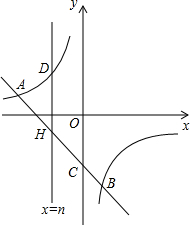
 如图,已知直线l:y=ax+b与反比例函数y=-$\frac{4}{x}$的图象交于A(-4,1)、B(m,-4),且直线l与y轴交于点C.
如图,已知直线l:y=ax+b与反比例函数y=-$\frac{4}{x}$的图象交于A(-4,1)、B(m,-4),且直线l与y轴交于点C.分析 (1)利用反比例函数图象上点的坐标特征求得m的值;然后将点A、B的坐标分别代入一次函数解析式,列出关于系数的方程组,通过解方程组求得它们的值即可;
(2)结合图象写出答案;
(3)需要分类讨论:当-4<n<0时和n<-4时两种情况下的三角形的面积的计算.
解答  解:(1)∵$y=-\frac{4}{x},B(m,-4)$,
解:(1)∵$y=-\frac{4}{x},B(m,-4)$,
∴m=1,
∴B(1,-4).
∵y=ax+b过A(-4,1),B(1,-4),
∴$\left\{\begin{array}{l}-4a+b=1\\ a+b=-4\end{array}\right.$,
解得$\left\{\begin{array}{l}a=-1\\ b=-3\end{array}\right.$,
∴直线解析式为y=-x-3;
(2)由函数图象可知,不等式ax+b>-$\frac{4}{x}$成立,则x的取值范围是x<-4或0<x<1.
故答案是:x<-4或0<x<1;
(3)∵直线与y轴交点为(0,-3),
∴${S_{△OAC}}=\frac{1}{2}×3×4=6$
由直线x=n可知$D({n,-\frac{4}{n}}),H(n,-n-3)$
当-4<n<0时,$DH=-\frac{4}{n}-(-n-3)=-\frac{4}{n}+n+3$,
∵${S_{△ODH}}=\frac{1}{2}{S_{△OAC}}=\frac{1}{2}×6=3$,
∴$\frac{1}{2}DH•(-n)=3$$即\frac{1}{2}(-\frac{4}{n}+n+3)•(-n)=3$,
整理得n2+3n+2=0,
解得:n1=-1,n2=-2;
当n<-4时,$DH=(-n-3)-(-\frac{4}{n})=-n-3+\frac{4}{n}$,
∵${S_{△ODH}}=\frac{1}{2}{S_{△OAC}}=\frac{1}{2}×6=3$,
∴$\frac{1}{2}DH•(-n)=3$$即\frac{1}{2}(-n-3+\frac{4}{n})•(-n)=3$,
整理得n2+3n-10=0,
解得:n1=-5,n2=2(不合题意,舍去).
综上可知n的值为-1,-2,-5.
点评 本题考查了一次函数与反比例函数交点问题,解题时,采用了分类讨论和数形结合的数学思想,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
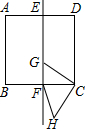 如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )
如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )| A. | $\frac{1}{2}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
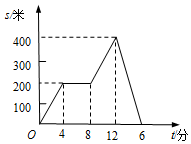 小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.
小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
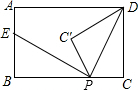 如图,在矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落在点C’处,作么BPC'的角平分线交AB于点E.设BP=x,BE=y,给出如下结论:
如图,在矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落在点C’处,作么BPC'的角平分线交AB于点E.设BP=x,BE=y,给出如下结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
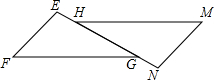 如图,△EFG≌△NMH,∠F和∠M是对应角.在△NMH中,MH是最长边.在△EFG中,FG是最长边,EF=2.1cm,EH=1.2cm,NH=4.4cm.
如图,△EFG≌△NMH,∠F和∠M是对应角.在△NMH中,MH是最长边.在△EFG中,FG是最长边,EF=2.1cm,EH=1.2cm,NH=4.4cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com