Question

6．已知等腰三角形的两边分别是2和4，则该三角形面积是$\sqrt{15}$．

Answer 1

分析 根据三角形两边之和大于第三边可得此等腰三角形腰长为4，底边长为2，然后画出图形，作出高，利用等腰三角形三线合一的性质可得BD长，利用勾股定理计算出AD长，然后可得面积．

解答 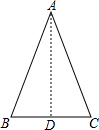解：根据三角形的三边关系得：此等腰三角形腰长为4，底边长为2，
如图所示：AB=AC=4，BC=2，
过A作AD⊥BC，
∵AB=AC，
∴BD=$\frac{1}{2}$BC=1，
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{15}$，
∴该三角形面积是：$\frac{1}{2}×$BC×AD=$\frac{1}{2}×$2×$\sqrt{15}$=$\sqrt{15}$，
故答案为：$\sqrt{15}$．

点评 此题主要考查了勾股定理，以及等腰三角形的性质，关键是正确利用勾股定理计算出高AD的长．