
【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.

(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.
【答案】(1)2![]() .(2)存在,2.(3)
.(2)存在,2.(3)![]() π.
π.
【解析】
试题分析:(1)过点C作CE⊥AB于E,根据CE=BCsin∠B求出CE,再根据AD=CE即可求出AD;
(2)若以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似,则△PCB必有一个角是直角.分两种情况讨论:①当∠PCB=90°时,求出AP,再根据在Rt△ADP中∠DPA=60°,得出∠DPA=∠B,从而得到△ADP∽△CPB,②当∠CPB=90°时,求出AP=3,根据![]() 且
且![]() ,得出△PCB与△ADP不相似.
,得出△PCB与△ADP不相似.
(3)先求出S1=π![]() ,再分两种情况讨论:
,再分两种情况讨论:
①当2<x<10时,作BC的垂直平分线交BC于H,交AB于G;作PB的垂直平分线交PB于N,交GH于M,连结BM,在Rt△GBH中求出BG、BN、GN,在Rt△GMN中,求出MN=![]() ,在Rt△BMN中,求出BM2=
,在Rt△BMN中,求出BM2=![]() ,最后根据S1=πBM2代入计算即可.
,最后根据S1=πBM2代入计算即可.
②当0<x≤2时,S2=π(![]() ),最后根据S=S1+S2=
),最后根据S=S1+S2=![]() π
π![]() π即可得出S的最小值.
π即可得出S的最小值.
试题解析:(1)过点C作CE⊥AB于E,
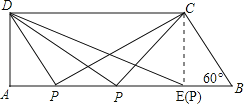
在Rt△BCE中,
∵∠B=60°,BC=4,
∴CE=BCsin∠B=4×![]() =2
=2![]() ,
,
∴AD=CE=2![]() .
.
(2)存在.若以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似,
则△PCB必有一个角是直角.
①当∠PCB=90°时,在Rt△PCB中,BC=4,∠B=60°,PB=8,
∴AP=AB-PB=2.
又由(1)知AD=2![]() ,在Rt△ADP中,tan∠DPA=
,在Rt△ADP中,tan∠DPA=![]() =
=![]() ,
,
∴∠DPA=60°,
∴∠DPA=∠CPB,
∴△ADP∽△CPB,
∴存在△ADP与△CPB相似,此时x=2.
②∵当∠CPB=90°时,在Rt△PCB中,∠B=60°,BC=4,
∴PB=2,PC=2![]() ,
,
∴AP=8.
则![]() 且
且![]() ,此时△PCB与△ADP不相似.1
,此时△PCB与△ADP不相似.1
(3)如图,因为Rt△ADP外接圆的直径为斜边PD,则S1=π(![]() )2=π
)2=π![]() ,
,
①当2<x<10时,作BC的垂直平分线交BC于H,交AB于G;
作PB的垂直平分线交PB于N,交GH于M,连结BM.则BM为△PCB外接圆的半径.
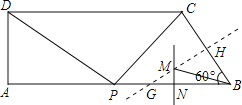
在Rt△GBH中,BH=![]() BC=2,∠MGB=30°,
BC=2,∠MGB=30°,
∴BG=4,
∵BN=![]() PB=
PB=![]() (10-x)=5-
(10-x)=5-![]() x,
x,
∴GN=BG-BN=![]() x-1.
x-1.
在Rt△GMN中,∴MN=GNtan∠MGN=![]() .
.
在Rt△BMN中,BM2=MN2+BN2=![]() ,
,
∴S2=πBM2=π(![]() ).
).
②∵当0<x≤2时,S2=π(![]() )也成立,
)也成立,
∴S=S1+S2=π![]() +π(
+π(![]() )=
)=![]() π
π![]() π.
π.
∴当x=![]() 时,S=S1+S2取得最小值
时,S=S1+S2取得最小值![]() π.
π.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
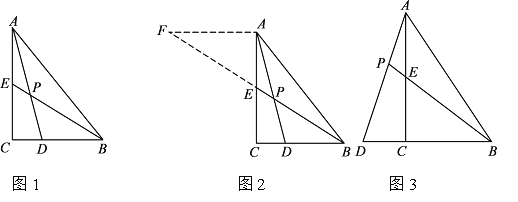
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题:

(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线x=﹣4与x轴交于点E,一开口向上的抛物线过原点交线段OE于点A,交直线x=﹣4于点B,过B且平行于x轴的直线与抛物线交于点C,直线OC交直线AB于D,且AD:BD=1:3.
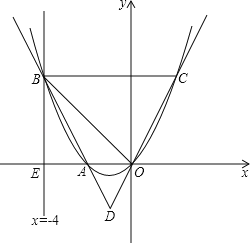
(1)求点A的坐标;
(2)若△OBC是等腰三角形,求此抛物线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.

(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
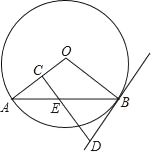
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
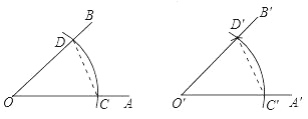
【题目】已知,∠AOB . 求作:∠A′O′B′,使∠A′O′B′=∠AOB . 作法:
①以________为圆心,________为半径画弧.分别交OA , OB于点C , D .
②画一条射线O′A′,以________为圆心,________长为半径画弧,交O′A′于点C′,
③以点________为圆心________长为半径画弧,与第2步中所画的弧交于点D′.
④过点________画射线O′B′,则∠A′O′B′=∠AOB .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形的变化过程,解答以下问题:


如图,在△ABC中,D为BC边上的一动点(D点不与B、C两点重合).DE∥AC交AB于E点,DF∥AB交AC于F点.
(小题1)试探索AD满足什么条件时,四边形AEDF为菱形,并说明理由;
(小题2)在(1)的条件下,△ABC满足什么条件时,四边形AEDF为正方形?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com