Question

在平面直角坐标系xOy中，关于y轴对称的抛物线 与x轴交于A、B 两点（点A在点B的左侧），与y轴交于点C，P是这条抛物线上的一点（点P不在坐标轴上），且点P关于直线BC的对称点在x轴上，D（0，3）是y轴上的一点．

（1）求抛物线的解析式及点P的坐标；

（2）若E、F是 y 轴负半轴上的两个动点（点E 在点F的上面），且EF＝2，当四边形PBEF的周长最小时，求点E、F的坐标；

（3）若Q是线段AC上一点,且，M是直线DQ上的一个动点，在x轴上方的平面内存在一点N，使得以 O、D、M、N为顶点的四边形是菱形，请你直接写出点N的坐标．

 

Answer 1

解：（1）∵抛物线关于y轴对称,

∴m－2=0．

∴m=2．

∴抛物线的解析式是.

令y＝0，得.

∴，．

在Rt△中，OC＝1, OB＝,可得∠OBC＝30º.

在Rt△中，OD＝3, OB＝,可得∠OBD＝60º.

∴BC是∠OBD的角平分线.

∴直线BD与x轴关于直线BC对称.

因为点P关于直线BC的对称点在x轴上，

则符合条件的点P就是直线BD与抛物线 的交点.

设直线BD的解析式为.

∴  ∴

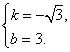
∴直线BD的解析式为.

∵点P在直线BD上，设P点坐标为.

又因为点P 在抛物线上，

∴.

解得.

∴.

∴点P的坐标是.

（2）过点P作PG⊥ 轴于G，在PG上截取，连结AH与轴交于点，在轴的负半轴上截取.

∵ PH∥EF，，

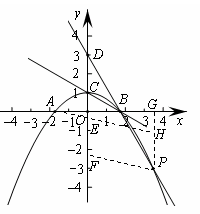∴ 四边形为平行四边形，有.

又 ∵ 、的长为定值，

∴ 此时得到的点、使四边形的周长最小.

∵ OE∥GH，

∴ Rt△∽Rt△.

∴ .

∴ .

∴ .

∴ 点的坐标为（0，），点的坐标为（0，）.

（3）点N的坐标是或或.