
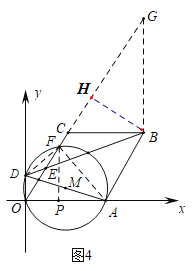
ЁОЬтФПЁПШчЭМЃЌвбжЊЦНУцжБНЧзјБъЯЕжаЃЌЕуCЃЈ3ЃЌ4ЃЉЃЌвдOCЮЊБпзїСтаЮOABCЃЌЧвЕуAТфдкxжсЕФе§АыжсЩЯЃЌЕуDЮЊyжсЩЯЕФвЛИіЖЏЕуЃЌЩшDЃЈ0ЃЌmЃЉЃЌСЌНсDBЃЌНЛжБЯпOCгкЕуEЃЎ
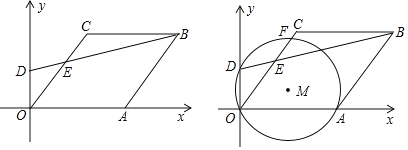
ЃЈ1ЃЉЬюПеЃКBЕФзјБъЮЊЃЈЁЁ ЁЁЃЉЃЌsinЁЯAOCЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЕБЕуDдкyжсе§АыжсЪБЃЌМЧЁїDEOЕФУцЛ§ЮЊS1ЃЌЁїBCEЕФУцЛ§ЮЊS2ЃЌЕБS1ЃНS2ЪБЃЌЧѓmЕФжЕЃЎ
ЃЈ3ЃЉЙ§ЕуDЃЌOЃЌAзїЁбMЃЌНЛЯпЖЮOCгкЕуFЃЎ
ЂйЕБЁбMгыСтаЮOABCвЛБпЫљдкЕФжБЯпЯрЧаЪБЃЌЧѓЫљгаТњзуЬѕМўЕФmЕФжЕЃЎ
ЂкЕБODЃНDEЪБЃЌжБНгаДГіOE:EFЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ8ЃЌ4ЃЉЃЌ![]() ЃЛЃЈ2ЃЉmЃН
ЃЛЃЈ2ЃЉmЃН![]() ЃЛЃЈ3ЃЉЂйТњзуЬѕМўЕФmЕФжЕЮЊ
ЃЛЃЈ3ЃЉЂйТњзуЬѕМўЕФmЕФжЕЮЊ![]() Лђ
Лђ![]() ЃЛЂкOE:EFЕФжЕ8:5ЃЎ
ЃЛЂкOE:EFЕФжЕ8:5ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌзїCHЁЭOAгкHЃЎИљОнЕуCЕФзјБъЧѓГіOHЃЌCH РћгУЙДЙЩЖЈРэЧѓГіOCМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉШчЭМ1жаЃЌбгГЄBCНЛODгкFЃЎгЩS1=S2ЃЌЭЦГіSЁїOCF=SЁїBDFЃЌгЩДЫЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЂйЗжСНжжЧщаЮЃКШчЭМ2жаЃЌЕБЁбMгыBCЯрЧаЪБЃЌИљОнPQ=DMЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎШчЭМ3жаЃЌЕБЁбMгыABЯрЧаЪБЃЌADЁЭABЃЌЩшADНЛOCгкQЃЎИљОнtamЁЯOAD=tanЁЯDOC=![]() ЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЂкШчЭМ4жаЃЌзїBGЁЭBCНЛOCЕФбгГЄЯпгкGЃЌСЌНгDFЃЌAFЃЌзїFPЁЭOAгкPЃЎЪзЯШЧѓГіBGЃЌдйжЄУїBE=BGЃЌИљОнDE+BE=BDЃЌЙЙНЈЗНГЬЧѓГіmЃЌЩшOF=5kЃЌдђFP=4kЃЌOP=3kЃЌдкRtЁїAPFжаЃЌИљОнAF2=PF2+PA2ЃЌЙЙНЈЗНГЬЧѓГіkМДПЩНтОіЮЪЬтЃЎ
ЃЈ1ЃЉШчЭМ1жаЃЌзїCHЁЭOAгкHЃЎ
ЁпC(3ЃЌ4)ЃЌCHЁЭOAЃЌ
ЁрOHЃН3ЃЌCHЃН4ЃЌ
ЁрOCЃН![]() ЃН
ЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрOAЃНABЃНOCЃНBCЃН5ЃЌBCЁЮOAЃЌ
ЁрB(8ЃЌ4)ЃЌ
ЁрsinЁЯAOCЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
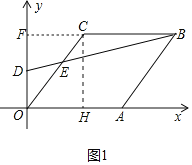
ЃЈ2ЃЉШчЭМ1жаЃЌбгГЄBCНЛODгкFЃЎ
ЁпS1ЃНS2ЃЌ
ЁрSЁїOCFЃНSЁїBDFЃЌ
Ёр![]() ЁС3ЁС4ЃН
ЁС3ЁС4ЃН![]() ЁС(4Љm)ЁС8ЃЌ
ЁС(4Љm)ЁС8ЃЌ
НтЕУmЃН![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЂйШчЭМ2жаЃЌбгГЄBCНЛODгкPЃЌзїMQЁЭODгкQЃЎ
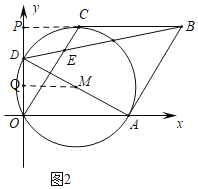
ЕБЁбMгыBCЯрЧаЪБЃЌPQЃНDMЃЎ
дђга4Љ![]() ЃН
ЃН![]()
![]() ЃЌ
ЃЌ
НтЕУmЃН![]() ЃЎ
ЃЎ
ШчЭМ3жаЃЌЕБЁбMгыABЯрЧаЪБЃЌADЁЭABЃЌЩшADНЛOCгкQЃЎ
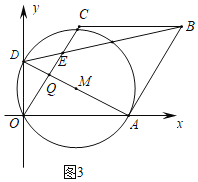
ЁпOC//ABЃЌ
ЁрOCЁЭADЃЌ
ЁрЁЯAQDЃН90ЁуЃЌ
ЁрЁЯDOQ+ЁЯAOQЃН90ЁуЃЌЁЯAOQ+ЁЯOAQЃН90ЁуЃЌ
ЁрЁЯDOQЃНЁЯOAQЃЌ
ЁрtamЁЯOADЃНtanЁЯDOCЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрmЃН![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФmЕФжЕЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЂкШчЭМ4жаЃЌзїBGЁЭBCНЛOCЕФбгГЄЯпгкGЃЌСЌНгDFЃЌAFЃЌзїBHЁЭOGгкHЃЌзїFPЁЭOAгкPЃЎ
ЁпBC//OAЃЌ
ЁрtanЁЯGCBЃНtanЁЯCOAЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрBGЃН![]() ЃЌ
ЃЌ
ЁпOD//BGЃЌ
ЁрЁЯGЃНЁЯDOEЃЌ
ЁпDOЃНEDЃЌ
ЁрЁЯDOEЃНЁЯDEOЃНЁЯBEGЃЌ
ЁрЁЯGЃНЁЯBEGЃЌ
ЁрBEЃНBGЃН![]() ЃЌ
ЃЌ
ЁпDE+BEЃНBDЃЌ
Ёр(m+![]() )2ЃН82+(4Љm)2ЃЌ
)2ЃН82+(4Љm)2ЃЌ
НтЕУmЃН![]() ЃЌ
ЃЌ
ЩшOFЃН5kЃЌдђFPЃН4kЃЌOPЃН3kЃЌ
ЁпЁЯODFЃНЁЯDAFЃЌ
ЁрtanЁЯDAFЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрsinЁЯDAFЃН![]() ЃЌ
ЃЌ
ЁпADЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрAFЃН![]()
![]() ЃЌ
ЃЌ
дкRtЁїAPFжаЃЌЁпAF2ЃНPF2+PA2ЃЌ
Ёр![]() ЁС(m2+25)ЃН(4k)2+(5Љ3k)2ЃЌ
ЁС(m2+25)ЃН(4k)2+(5Љ3k)2ЃЌ
АбmЃН![]() ДњШыЃЌећРэЕУЃК45k2Љ54k+13ЃН0ЃЌ
ДњШыЃЌећРэЕУЃК45k2Љ54k+13ЃН0ЃЌ
НтЕУkЃН![]() ЃЈЩсШЅЃЉЛђ
ЃЈЩсШЅЃЉЛђ![]() ЃЌ
ЃЌ
ЁрOFЃН![]() ЃЎ
ЃЎ
ЁпsinЁЯGЃНsinЁЯDAFЃН![]() ЃЌ
ЃЌ
ЁрGH=![]() ЃЌ
ЃЌ
ЁрEG=2GH=![]() ЃЌ
ЃЌ
ЁпBG//ODЃЌ
ЁрЁїODEЁзЁїGBEЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпOEЃН![]() ЃЌ
ЃЌ
ЁрEFЃНOFЉOEЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
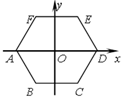
ЁОЬтФПЁПШчЭМЃЌе§СљБпаЮ ABCDEFЕФжааФгызјБъдЕуOжиКЯЃЌЦфжаA(-2ЃЌ0)ЃЎНЋСљБпаЮ ABCDEFШЦдЕуOАДЫГЪБеыЗНЯђа§зЊ2018ДЮЃЌУПДЮа§зЊ60ЁуЃЌдђа§зЊКѓЕуAЕФЖдгІЕуA'ЕФзјБъЪЧЃЈ ЃЉЃЎ
A. (1ЃЌ![]() ) B. (
) B. (![]() ЃЌ1) C. (1ЃЌ
ЃЌ1) C. (1ЃЌ![]() ) D. (-1ЃЌ
) D. (-1ЃЌ![]() )
)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЕРзїЭМЬтШчЯТЃК
вбжЊЃКШчЭМ1ЃЌЁЯABCМАBCБпЩЯвЛЕуDЃЎ
ЧѓзїЃКвЛЕуPЃЌЪЙЕуPЕНЁЯABCСНБпЕФОрРыЯрЕШЃЌЧвЕНBЃЌDСНЕуЕФОрРыЯрЕШЃЎЯТУцЪЧвЛЮЛЭЌбЇЕФзїЭМЙ§ГЬЃЈЭМ2ЃЉЃК
ЃЈ1ЃЉзїЁЯABCЕФЦНЗжЯпBEЃЛ
ЃЈ2ЃЉзїЯпЖЮBDЕФДЙжБЦНЗжЯпlЃЌгыBEНЛгкЕуPЃЎ
ЫљвдЕуPОЭЪЧЫљЧѓзїЕФЕуЃЎдђИУзїЭМЕФвРОнЪЧ___________________________________ЃЎ
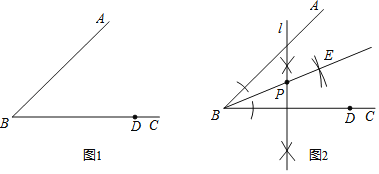
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
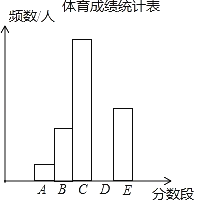
ЁОЬтФПЁПЮЊСЫСЫНтФГЪаОХФъМЖбЇЩњЕФЬхг§ГЩМЈЃЈГЩМЈОљЮЊећЪ§ЃЉЃЌЫцЛњГщШЁСЫВПЗжбЇЩњЕФЬхг§ГЩМЈВЂЗжЖЮЃЈAЃК20.5ЁЋ22.5ЃЛBЃК22.5ЁЋ24.5ЃЛCЃК24.5ЁЋ26.5ЃЛDЃК26.5ЁЋ28.5ЃЛEЃК28.5ЁЋ30.5ЃЉЭГМЦЃЌЕУЕНЭГМЦЭМЁЂБэШчЭМЃЎ
ЗжЪ§ЖЮ | A | B | C | D | E | КЯМЦ |
ЦЕЪ§/ШЫ | 12 | 36 | 84 | b | 48 | c |
ЦЕТЪ | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
ИљОнЩЯУцЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЭГМЦБэжаЃЌaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЌcЃНЁЁ ЁЁЃЛНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЎ
ЃЈ2ЃЉаЁУїЫЕЃКЁАетзщЪ§ОнЕФжкЪ§вЛЖЈдкCжаЃЎЁБФуШЯЮЊаЁУїЕФЫЕЗЈе§ШЗТ№ЃПЁЁ ЁЁЃЈбЁЬюЁАе§ШЗЁБЛђЁАДэЮѓЁБЃЉЃЎ
ЃЈ3ЃЉШєГЩМЈдк27ЗжМАвдЩЯЖЈЮЊгХауЃЌдђИУЪа30000УћОХФъМЖбЇЩњжаЬхг§ГЩМЈЮЊгХауЕФбЇЩњШЫЪ§дМгаЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
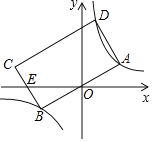
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDЕФЖЅЕуAЃЌBЃЌDЗжБ№ТфдкЫЋЧњЯпyЃН![]() ЃЈkЃО0ЃЉЕФСНИіЗжжЇЩЯЃЌABБпОЙ§дЕуOЃЌCBБпгыxжсНЛгкЕуEЃЌЧвECЃНEBЃЌШєЕуAЕФКсзјБъЮЊ1ЃЌдђОиаЮABCDЕФУцЛ§_____ЃЎ
ЃЈkЃО0ЃЉЕФСНИіЗжжЇЩЯЃЌABБпОЙ§дЕуOЃЌCBБпгыxжсНЛгкЕуEЃЌЧвECЃНEBЃЌШєЕуAЕФКсзјБъЮЊ1ЃЌдђОиаЮABCDЕФУцЛ§_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп ![]() гы
гы ![]() жсНЛгк
жсНЛгк![]() КЭ
КЭ![]() ЃЌгы
ЃЌгы ![]() жсНЛгк
жсНЛгк ![]() ЕуЃЌЕу
ЕуЃЌЕу![]() ЙигкХзЮяЯпЕФЖдГЦжсЕФЖдГЦЕуЮЊЕу
ЙигкХзЮяЯпЕФЖдГЦжсЕФЖдГЦЕуЮЊЕу![]() ЃЎ
ЃЎ
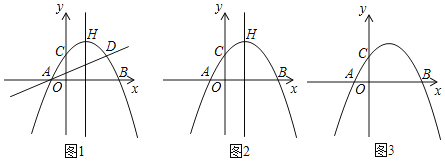
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНКЭЖдГЦжсЃЎ
ЃЈ2ЃЉШчЭМ 2ЃЌЕБЕу![]() дкХзЮяЯпЕФЖдГЦжсЩЯдЫЖЏЪБЃЌдкжБЯп
дкХзЮяЯпЕФЖдГЦжсЩЯдЫЖЏЪБЃЌдкжБЯп![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУвдЕу
ЃЌЪЙЕУвдЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіЕу
ЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіЕу ![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ 3ЃЌЕБЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЙВдВЪБЃЌЧыЧѓГіИУдВдВаФЕФзјБъЃЎ
Ш§ЕуЙВдВЪБЃЌЧыЧѓГіИУдВдВаФЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫГДЮСЌНгЖдНЧЯпЯрЕШЕФЫФБпаЮИїБпжаЕуЃЌЫљЕУЫФБпаЮЪЧ( )
A. ОиаЮ B. ЦНааЫФБпаЮ C. СтаЮ D. ШЮвтЫФБпаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъЯњЪл10ЬЈAаЭКЭ20ЬЈBаЭЕчФдЕФРћШѓЮЊ4000дЊЃЌЯњЪл20ЬЈAаЭКЭ10ЬЈBаЭЕчФдЕФРћШѓЮЊ3500дЊЃЎ
ЃЈ1ЃЉЧѓУПЬЈAаЭЕчФдКЭBаЭЕчФдЕФЯњЪлРћШѓЃЛ
ЃЈ2ЃЉИУЩЬЕъМЦЛЎвЛДЮЙКНјСНжжаЭКХЕФЕчФдЙВ100ЬЈЃЌЦфжаBаЭЕчФдЕФНјЛѕСПВЛГЌЙ§AаЭЕчФдЕФ2БЖЃЌЩшЙКНјAаЭЕчФдxЬЈЃЌет100ЬЈЕчФдЕФЯњЪлзмРћШѓЮЊyдЊЃЎ
ЂйЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкИУЩЬЕъЙКНјAаЭЁЂBаЭЕчФдИїЖрЩйЬЈЃЌВХФмЪЙЯњЪлзмРћШѓзюДѓЃП
ЃЈ3ЃЉЪЕМЪНјЛѕЪБЃЌГЇМвЖдAаЭЕчФдГіГЇМлЯТЕїmЃЈ0ЃМmЃМ100ЃЉдЊЃЌЧвЯоЖЈЩЬЕъзюЖрЙКНјAаЭЕчФд70ЬЈЃЌШєЩЬЕъБЃГжЭЌжжЕчФдЕФЪлМлВЛБфЃЌЧыФуИљОнвдЩЯаХЯЂМАЃЈ2ЃЉжаЬѕМўЃЌЩшМЦГіЪЙет100ЬЈЕчФдЯњЪлзмРћШѓзюДѓЕФНјЛѕЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
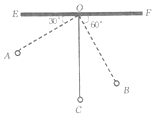
ЁОЬтФПЁПШчЭМЃЌЮяРэНЬЪІЮЊЭЌбЇУЧбнЪОЕЅАкдЫЖЏЃЌЕЅАкзѓгвАкЖЏжаЃЌдк![]() ЕФЮЛжУЪБИЉНЧ
ЕФЮЛжУЪБИЉНЧ![]() ЃЌдк
ЃЌдк![]() ЕФЮЛжУЪБИЉНЧ
ЕФЮЛжУЪБИЉНЧ![]() ЃЌШє
ЃЌШє![]() ЃЌЕу
ЃЌЕу![]() БШЕу
БШЕу![]() Ип7
Ип7![]() ЃЎ
ЃЎ
ЧѓЃКЃЈ1ЃЉЕЅАкЕФГЄЖШЃЛ
ЃЈ2ЃЉДгЕу![]() АкЖЏЕНЕу
АкЖЏЕНЕу![]() ОЙ§ЕФТЗОЖГЄЃЎЃЈвЊЧѓЃКБОЬтжаЕФМЦЫуНсЙћОљБЃСєећЪ§ЃЎВЮПМжЕЃК
ОЙ§ЕФТЗОЖГЄЃЎЃЈвЊЧѓЃКБОЬтжаЕФМЦЫуНсЙћОљБЃСєећЪ§ЃЎВЮПМжЕЃК![]() ЃЛ
ЃЛ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com