
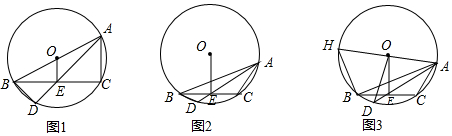
分析 (1)依据垂径定理可得到BE=EC,从而可得到OE是△ABC的中位线,依据三角形的中位线定理可知OE=$\frac{1}{2}$AC,依据直径所对的圆周角等于90°可得到∠BCA=90°,依据EC=AC可得到∠AEC=45°,于是可证明△EBD是等腰直角三角形,故此可得到BE=$\sqrt{2}$BD,从而得到BD与OE的关系;
(2)依据等腰三角形的性质可得到∠CAE=∠CEA,依据圆周角定理的推理得到∠DBC=∠EAC,依据三角形的外角的性质可知∠CBA+∠BAE=∠AEC,最后在△ABC中依据三角形的内角和定理证明即可;
(3)如图3,过点O作OM⊥AC于点M,过点D作DK⊥BC于点K、DG⊥OE交OE延长线于点G,连接OC,过点A作AP⊥BC交BC延长线于点P,由△OAM≌△ODG,推出∠DOG=∠AOM,由tan∠AOM=tan∠DOG=$\frac{AM}{OM}$=$\frac{\sqrt{3}}{5}$,求出OM、OA、AH,由tan∠ABC=tan∠AOM=$\frac{AP}{BP}$=$\frac{\sqrt{3}}{5}$,设AP=$\sqrt{3}$a,BP=5a,则CP=5a-4,AP2+CP2=AC2,列出方程求出a,再在Rt△ABH中,利用勾股定理求出BH即可.
解答 解:(1)如图1中,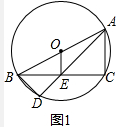
∵OE⊥BC,
∴BE=EC.
∵OA=OB,
∴OE=$\frac{1}{2}$AC.
∵AB为直径,
∴∠ADB=∠ACB=90°.
∵AC=CE,
∴∠CAE=∠BED=45°.
∵sin∠BED=$\frac{BD}{BE}$=$\frac{\sqrt{2}}{2}$,
∴BE=CE=AC=$\sqrt{2}$BD,
∴BD=$\sqrt{2}$OE.
(2)如图2中,
∵AC=CE,
∴∠CAE=∠CEA,
∵∠DBC=∠EAC,
∴∠DBC+∠CEA+∠ACB=180°,
∴∠C+2∠DBC=180°;
(3)解:如图3,过点O作OM⊥AC于点M,过点D作DK⊥BC于点K、DG⊥OE交OE延长线于点G,连接OC,过点A作AP⊥BC交BC延长线于点P.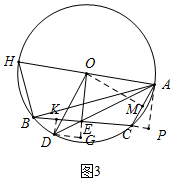
由(2)得:BE=CE=AC=$\frac{1}{2}$BC=2,
∵OA=OC,
∴AM=CM=1,
∵BD=DE,
∴BK=KE=1,
∵∠DKE=∠DGE=∠GEK=90°,四边形DKEG为矩形,
∴DG=1,
∵OA=OD,
∴△OAM≌△ODG,
∴∠DOG=∠AOM,
∴tan∠AOM=tan∠DOG=$\frac{AM}{OM}$=$\frac{\sqrt{3}}{5}$,
∵AM=1,
∴OM=$\frac{5\sqrt{3}}{3}$,
∴OA=$\sqrt{A{M}^{2}+O{M}^{2}}$=$\frac{2\sqrt{21}}{3}$,
∴AH=2OA=$\frac{4\sqrt{21}}{3}$,
∵∠AOC=2∠ABC,
∴∠ABC=∠AOM,
∵tan∠ABC=tan∠AOM=$\frac{AP}{BP}$=$\frac{\sqrt{3}}{5}$,
设AP=$\sqrt{3}$a,BP=5a,
∴CP=5a-4,
∵AP2+CP2=AC2,即($\sqrt{3}$a)2+(5a-4)2=22,
解得:a1=1,a2=$\frac{7}{3}$(舍去),
∴BP=5,AP=$\sqrt{3}$,AB=$\sqrt{A{P}^{2}+B{P}^{2}}$=2$\sqrt{7}$,
∴BH=$\sqrt{A{H}^{2}-A{B}^{2}}$=$\frac{2\sqrt{21}}{3}$.
点评 本题考查圆综合题、垂径定理、锐角三角函数、勾股定理、全等三角形的判定和性质、矩形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加辅助线,构造特殊三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
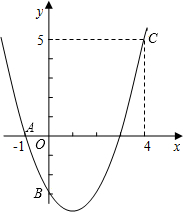 如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.
如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com