
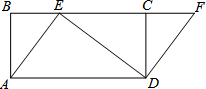
 如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE,求证:四边形AEFD是平行四边形.
如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE,求证:四边形AEFD是平行四边形. 分析 直接利用矩形的性质结合全等三角形的判定与性质得出BE=CF,进而得出答案.
解答 证明:∵四边形ABCD是矩形,
∴AB=DC,∠B=∠DCF=90°,
∵∠BAE=∠CDF,
在△ABE和△DCF中,$\left\{\begin{array}{l}{∠B=∠DCF}&{\;}\\{AE=DC}&{\;}\\{∠BAE=∠CDF}&{\;}\end{array}\right.$,
∴△ABE≌△DCF(ASA),
∴BE=CF,
∴BC=EF,
∵BC=AD,
∴EF=AD,
又∵EF∥AD,
∴四边形AEFD是平行四边形.
点评 此题主要考查了平行四边形的性质与判定、全等三角形的判定与性质;证明三角形全等是解决问题的关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:填空题
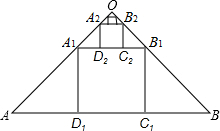 如图,等腰直角三角形OAB中,∠AOB=90°,AB=1,在△OAB中作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…;依次作下去,则第n个正方形AnBnCnDn的面积是$\frac{1}{{9}^{n}}$.
如图,等腰直角三角形OAB中,∠AOB=90°,AB=1,在△OAB中作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…;依次作下去,则第n个正方形AnBnCnDn的面积是$\frac{1}{{9}^{n}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
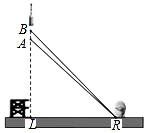 2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.
2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 组别 | A型 | B型 | AB型 | O 型 |
| 频率 | 0.4 | 0.35 | 0.1 | 0.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{2\sqrt{13}}{13}$ | D. | $\frac{3\sqrt{13}}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com