
分析 (1)观察阅读材料中的方程解过程,归纳总结得到结果;
(2)仿照方程解方程,归纳总结得到结果;
(3)方程变形后,利用得出的规律得到结果即可.
解答 解:(1)x+$\frac{20}{x}=-9$,其解为:x1=-4,x2=-5,
故答案为:x+$\frac{20}{x}$=-9,x1=-4,x2=-5;
(2)x+$\frac{{n}^{2}+n}{x}$=-(2n+1),其解为:x1=-n,x2=-n-1,
故答案为:x+$\frac{{n}^{2}+n}{x}$=-(2n+1),x1=-n,x2=-n-1;
(3)x+$\frac{{n}^{2}+n}{x+3}$=-2(n+2)
x+3+$\frac{{n}^{2}+n}{x+3}$=-2(n+2)+3
(x+3)+$\frac{{n}^{2}+n}{x+3}$=-(2n+1)
∴x+3=-n或x+3=-(n+1)
即:x1=-n-3,x2=-n-4.
点评 此题考查了分式方程的解,方程的解即为能使方程左右两边相等的未知数的值.弄清题中的规律是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
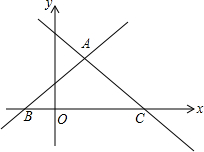 如图,在平面直角坐标系中,直线y=x+1与直线y=-$\frac{3}{4}$x+3,交于点A($\frac{8}{7}$,$\frac{15}{7}$),且两直线分别交x轴于B,C两点.
如图,在平面直角坐标系中,直线y=x+1与直线y=-$\frac{3}{4}$x+3,交于点A($\frac{8}{7}$,$\frac{15}{7}$),且两直线分别交x轴于B,C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,AB,CD相交于O点,OE是∠COB的平分线,FO⊥OE,且∠AOD=60°.
如图所示,AB,CD相交于O点,OE是∠COB的平分线,FO⊥OE,且∠AOD=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com