
 在平面直角坐标系中,我们把横纵坐标都是整数的点叫做整点,已知二次函数y=-$\frac{{x}^{2}}{3}$+4和反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象如图所示,它们围成的阴影部分(包括边界)的整点个数为5,则k的取值范围是( )
在平面直角坐标系中,我们把横纵坐标都是整数的点叫做整点,已知二次函数y=-$\frac{{x}^{2}}{3}$+4和反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象如图所示,它们围成的阴影部分(包括边界)的整点个数为5,则k的取值范围是( )| A. | 1<k≤2 | B. | 1<k<2 | C. | 0<k≤2 | D. | 1≤k≤2 |
分析 根据二次函数的解析式判断在第一象限内在二次函数图象下方或图象上的整点的个数,并写出它们的坐标,再结合反比例函数图象上点的坐标特征以及二次函数图象与反比例函数图象围成的部分(包括边界)的整点个数为5,即可得出k的取值范围.
解答 解:∵当x=1时,y=-$\frac{1}{3}$+4=$\frac{11}{3}$>3;当x=2时,y=-$\frac{4}{3}$+4=$\frac{8}{3}$>2;当x=3时,y=-3+4=1.
∴再第一象限内在二次函数y=-$\frac{{x}^{2}}{3}$+4的图象上和图象下方的整点有6个,坐标为(1,1)、(1,2)、(1,3)、(2,1)、(2,2),(3,1).
∵1×1=1,1×2=2,1×3=3,2×1=2,2×2=4,3×1=3,且在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上和上方的整点有5个,
∴整点(1,1)不在阴影区域内,
∴1<k≤2.
故选A.
点评 本题考查了二次函数图象上点的坐标特征以及反比例函数图象上点的坐标特征,解题的关键是找出整点的坐标.本题属于中档题,难度不大,解决该题型题目时,结合二次函数与反比例函数图象上点的坐标特征找出整点的坐标是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一次向右拐40°,第二次向左拐140° | |
| B. | 第一次向右拐40°,第二次向右拐140° | |
| C. | 第一次向左拐40°,第二次向左拐140° | |
| D. | 第一次向左拐40°,第二次向右拐40° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
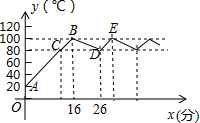 张老师办公室的饮水机具有自动调节功能,开机后自动进行加热状态,水温y(℃)与开机后用时x(分钟)成一次函数关系,当水温上升到100℃时停止加热,水温开始下降,此时水温y(℃)与开机后用时x(分钟)仍成一次函数某天早晨7:00时,张老师打开饮水机,水温变化情况如图所示.
张老师办公室的饮水机具有自动调节功能,开机后自动进行加热状态,水温y(℃)与开机后用时x(分钟)成一次函数关系,当水温上升到100℃时停止加热,水温开始下降,此时水温y(℃)与开机后用时x(分钟)仍成一次函数某天早晨7:00时,张老师打开饮水机,水温变化情况如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com