
【题目】从共享单车,共享汽车等共享出行到共享充电宝,共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速普及应用,越来越多的企业与个人成为参与者与受益者.根据国家信息中心发布的《中国分享经济发展报告2017》显示,2016年我国共享经济市场交易额约为34520亿元,比上年增长103%;超6亿人参与共享经济活动,比上年增加约1亿人.
如图是源于该报告中的中国共享经济重点领域市场规模统计图: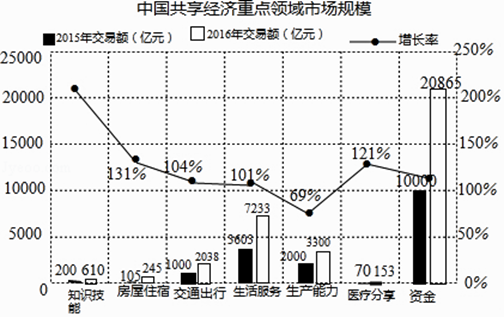
(1)请根据统计图解答下列问题:
①图中涉及的七个重点领域中,2016年交易额的中位数是亿元.
②请分别计算图中的“知识技能”和“资金”两个重点领域从2015年到2016年交易额的增长率(精确到1%),并就这两个重点领域中的一个分别从交易额和增长率两个方面,谈谈你的认识.
(2)小宇和小强分别对共享经济中的“共享出行”和“共享知识”最感兴趣,他们上网查阅了相关资料,顺便收集到四个共享经济领域的图标,并将其制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同)他们将这四张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号A,B,C,D表示)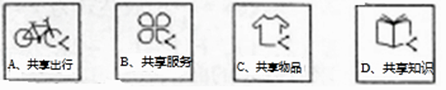
【答案】
(1)2038;①“知识技能”的增长率为: ![]() ×100%=205%,
×100%=205%,
②“资金”的增长率为: ![]() ≈109%,
≈109%,
由此可知,“知识技能”领域交易额较小,当增长率最高,达到200%以上,其发展速度惊人.
(2)
解:画树状图为:
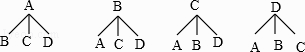
共有12种等可能的结果数,其中抽到“共享出行”和“共享知识”的结果数为2,
所以抽到“共享出行”和“共享知识”的概率= ![]() =
= ![]()
【解析】解:(1)由图可知,2016年七个重点领域的交易额分别为70、245、610、2038、3300、7233、20863,
2016年交易额的中位数是2038亿元,
所以答案是:2038;
【考点精析】关于本题考查的条形统计图和折线统计图,需要了解能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况;能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比才能得出正确答案.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
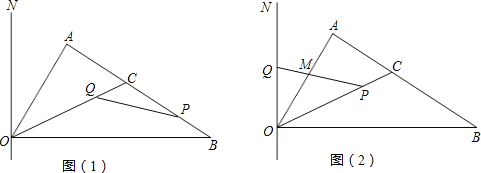
【题目】如图(1),Rt△AOB中,∠A=90°,∠AOB=60°,OB=![]() ,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
(1)求OC、BC的长;
(2)设△CPQ的面积为S,求S与t的函数关系式;
(3)当P在OC上Q在ON上运动时,如图(2),设PQ与OA交于点M,当t为何值时,△OPM为等腰三角形?求出所有满足条件的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 ![]() ,导致了第一次数学危机,
,导致了第一次数学危机, ![]() 是无理数的证明如下: 假设
是无理数的证明如下: 假设 ![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成 ![]() (p与q是互质的两个正整数).于是(
(p与q是互质的两个正整数).于是( ![]() )2=(
)2=( ![]() )2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“
)2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“ ![]() 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以, ![]() 是无理数.
是无理数.
这种证明“ ![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法
B.反证法
C.举反例法
D.数学归纳法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )
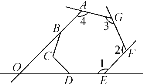
A. 400 B. 450 C. 500 D. 600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚在课外书中看到这样一道有理数的混合运算题:
计算:![]()
她发现,这个算式反映的是前后两部分的和,而这两部分之间存在着某种关系,利用这种关系,他顺利地解答了这道题。
(1)前后两部分之间存在着什么关系?
(2)先计算哪步分比较简便?并请计算比较简便的那部分。
(3)利用(1)中的关系,直接写出另一部分的结果。
(4)根据以上分析,求出原式的结果。
查看答案和解析>>
科目:初中数学 来源: 题型:
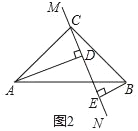
【题目】(1)探究证明:
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E,当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)发现探究:
当直线MN绕点C旋转到图2的位置时,(1)中的结论是否成立,如果不成立,DE、AD、BE应满足的关系是_____.
(3)解决问题:
当直线MN绕点C旋转到图3的位置时,若BE=8,AD=2,请直接写出DE的长为_____.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=70°,求∠DOE和∠EOF的度数;
(2)请写出图中∠AOD的补角和∠AOE的余角.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com