
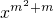 的图象是开口向下的抛物线.
的图象是开口向下的抛物线. ;
;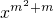 的图象是开口向下的抛物线,
的图象是开口向下的抛物线, 时,y随x的增大而减小;x>-
时,y随x的增大而减小;x>- 时,y随x的增大而增大;此时函数有最小值.
时,y随x的增大而增大;此时函数有最小值. 时,y随x的增大而增大;x>-
时,y随x的增大而增大;x>- 时,y随x的增大而减小;此时函数有最大值.
时,y随x的增大而减小;此时函数有最大值. 

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案科目:初中数学 来源: 题型:
 23、春林高级中学为了改善办学条件,2001年暑假对高中部内道长300米的操场投资修建塑胶跑道.请你根据图上所示数据完成下列各题(π取3.14):
23、春林高级中学为了改善办学条件,2001年暑假对高中部内道长300米的操场投资修建塑胶跑道.请你根据图上所示数据完成下列各题(π取3.14):查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
根据下列条件,解答下列各题.
(1)如果关于x的方程x+2m-3=3x+7的解为不大于2的非负数,求m的取值范围;
(2)若|3x-4|>3x-4,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com