
【题目】(1)如图1,在等边△ABC中,点M是BC边上的任意一点(不含端点B,C),连结AM,以AM为边作等边△AMN,并连结CN.求证:AB=CN+CM.
(2)(类比探究)如图2,在等边△ABC中,若点M是BC延长线上的任意一点(不含端点C),其它条件不变,则AB=CN+CM是否还成立?若成立,请说明理由;若不成立,请写出AB,CN,CM三者之间的数量关系,并给予证明.

【答案】(1)见解析;(2)不成立,AB=CN﹣CM,见解析
【解析】
(1)根据等边三角形的性质得到AB=BC=AC,∠BAC=∠B=∠ACB=60°,AM=MN=AN,∠MAN=∠AMN=∠ANM=60°,证明△BAM≌△CAN,根据全等三角形的性质、结合图形证明结论;
(2)仿照(1)的证明过程解答即可.
(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,∠BAC=∠B=∠ACB=60°,
∵△AMN是等边三角形,
∴AM=MN=AN,∠MAN=∠AMN=∠ANM=60°,
∴∠BAC﹣∠MAC=∠MAN﹣∠MAC,即∠BAM=∠CAN,
在△BAM和△CAN中,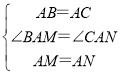 ,
,
∴△BAM≌△CAN(SAS)
∴BM=CN,
∴AB=BC=BM+CM=CN+CM;
(2)解:AB=CN+CM不成立,AB=CN﹣CM,
由(1)可知,∠BAC=∠MAN
∴∠BAC+∠MAC=∠MAN+∠MAC,即∠BAM=∠CAN,
在△BAM和△CAN中,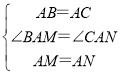 ,
,
∴△BAM≌△CAN(SAS)
∴BM=CN,
∴AB=BC=BM﹣CM=CN﹣CM.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的电脑,已知购买一台A型电脑需0.6万元,购买一台B型电脑需0.4万元,该公司准备投入资金y万元,全部用于购进35台这两种型号的电脑,设购进A型电脑x台.
(1)求y关于x的函数解析式;
(2)若购进B型电脑的数量不超过A型电脑数量的2倍,则该公司至少需要投入资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=x+|x﹣2|的图象与性质
小明根据学习函数的经验,对函数y=x+|x﹣2|的图象与性质进行了探究
下面是小明的探究过程,请补充完成:
(1)化简函数解析式,当x≥2时,y= ;当x<2时,y= ;
(2)根据(1)中的结果,请在图1的坐标系中画出函数y=x+|x﹣2|的图象;
(3)结合函数的图象,写出该函数的一条性质: ;
(4)结合画出的函数图象,利用图2解决问题,若关于x的方程ax+1=x+|x﹣2|有两个实数根,直接写出实数a的取值范围: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级的小明同学通到这样一道数学题目:△ABC为边长为4的等边三角形,E是边AB边上任意一动点,点D在CB的延长线上,且满足AE=BD.

(1)如图①,当点E为AB的中点时,DE= ;
(2)如图②,点E在运动过程中,DE与EC满足什么数量关系?请说明理由;
(3)如图③,F是AC的中点,连接EF.在AB边上是否存在点E,使得DE+EF值最小?若存在,求出这个最小值;若不存在,请说明理由.(直角三角形中,30°所对的边是斜边的一半)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)求点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,点![]() ,点
,点![]() 是
是![]() 轴上方的点,且
轴上方的点,且![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() .
.

(1)当![]() 时,求
时,求![]() 的长.
的长.
(2)求证:![]() .
.
(3)若![]() 的中点为
的中点为![]() ,探究点
,探究点![]() 横坐标的规律.
横坐标的规律.
特殊情况探究:①当![]() 时,求出此时点
时,求出此时点![]() 的横坐标为6,②当
的横坐标为6,②当![]() 时,求得此时点
时,求得此时点![]() 的横坐标为______.
的横坐标为______.
一般情况探究:③当![]() 时,点
时,点![]() 横坐标的规律是什么?并证明这个规律.
横坐标的规律是什么?并证明这个规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国著名的数学著作《九章算术》中的一个问题,“今有圆材,埋于壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?” 用现代的数学语言表达是:“如图,CD是⊙O的直径,弦AB⊥CD,垂足为E,CE = 1寸,AB = 1尺,求直径的长”. 依题意,CD长为( )
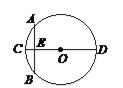
A. ![]() 寸 B. 13寸 C. 25寸 D. 26寸
寸 B. 13寸 C. 25寸 D. 26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
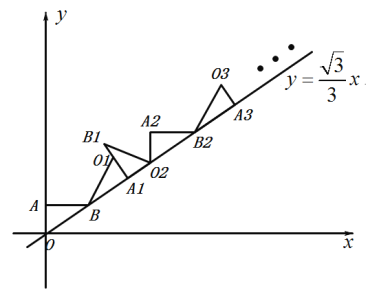
【题目】如图,在平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,使点
的位置,使点![]() 对应点
对应点![]() 落在直线
落在直线![]() 上,再将
上,再将![]() 绕点
绕点![]() 旋转到
旋转到![]() 的位置,使点
的位置,使点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上,依次进行下去…,若点
上,依次进行下去…,若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的横坐标为___________.
的横坐标为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com