
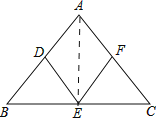
【题目】如图,点D、E、F分别是△ABC各边中点,若AB=AC=10,BC=12,求四边形ADEF的周长和面积.

【答案】周长为20,面积为24.
【解析】
试题根据三角形的中位线定理可得DE∥AC,EF∥AB,再根据两组对边分别平行的四边形ADEF是平行四边形,从而得AD=EF,AF=DE,所以四边形ADEF的周长=AB+AC,连接AE,则AE⊥BC,根据勾股定理可求出AE的长,进而得到三角形ABC的面积,因为四边形ADEF的面积是三角形面积的一半,问题得解.
试题解析:∵D、E分别为AB、BC的中点,
∴DE∥AC,
∵E、F分别为BC、AC中点,
∴EF∥AB,
∴四边形ADEF是平行四边形;
∴AD=EF,AF=DE,
∵点D、E、F分别是△ABC各边中点,AB=AC,
∴AD=DB=AF=FC,
∴四边形ADEF的周长=AB+AC=20,
连接AE,则AE⊥BC,BE=![]() BC=
BC=![]() =6,
=6,
∴AE=![]() =8,
=8,
∴S△ABC=![]() ×12×8=48,
×12×8=48,
∴S四边形ADEF=![]() ×48=24.
×48=24.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求a的值和直线AB的函数表达式;
(2)设△PMN的周长为C1 , △AEN的周长为C2 , 若 ![]() =
= ![]() ,求m的值;
,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E′A、E′B,求E′A+ ![]() E′B的最小值.
E′B的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚家、公交车站、学校在一条笔直的公路旁(小刚家、学校到这条公路的距离忽略不计)一天,小刚从家出发去上学,沿这条公路步行到公交站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小刚下车时发现还有4分钟上课,于是他沿着这条公路跑步赶到学校(上、下车时间忽略不计),小刚与学校的距离s(单位:米)与他所用的时间t(单位:分钟)之间的函数关系如图所示.已知小刚从家出发7分钟时与家的距离是1200米,从上公交车到他到达学校公用10分钟.下列说法:
①公交车的速度为400米/分钟;
②小刚从家出发5分钟时乘上公交车;
③小刚下公交车后跑向学校的速度是100米/分钟;
④小刚上课迟到了1分钟.
其中正确的个数是( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了8次测试,测试成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 10 | 8 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | 8 | 10 |
(1)根据表格中的数据,计算出甲的平均成绩是 9 环,乙的平均成绩是 9 环;
(2)分别计算甲、乙两名运动员8次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形的一边长是9cm,那么这个平行四边形的两条对角线的长可以是( )
A. 4cm和6cm B. 6cm和8cm C. 8cm和10cm D. 10cm和12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在纪念中国抗日战争胜利70周年之际,某公司决定组织员工观看抗日战争题材的影片,门票有甲乙两种,甲种票比乙种票每张贵6元;买甲种票10张,乙种票15张共用去660元.
(1)求甲、乙两种门票每张各多少元?
(2)如果公司准备购买35张门票且购票费用不超过1000元,那么最多可购买多少张甲种票?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( ) 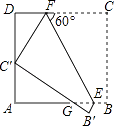
A.3 ![]() ﹣4
﹣4
B.4 ![]() ﹣5
﹣5
C.4﹣2 ![]()
D.5﹣2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com